Das Newton-Verfahren
h. geht gegen) die gesuchte exakte Lösung a.
Hilfreich wäre eine sogenannte Konvergenzbedingung für unseren Startwert, also irgendeine mathematische Bedingung, die absolut sicherstellt, dass sich die Näherungswerte 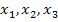 … immer mehr an die exakte Lösung annähern. (Streng genommen muss nicht nur der Startwert diese Konvergenzbedingung erfüllen, sondern auch jeder der Näherungswerte
… immer mehr an die exakte Lösung annähern. (Streng genommen muss nicht nur der Startwert diese Konvergenzbedingung erfüllen, sondern auch jeder der Näherungswerte 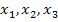 …)
…)
Konvergenzbedingung beim Newton-Verfahren:
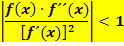
Leider ist diese Bedingung nur mit relativ großem Rechenaufwand zu überprüfen, so dass man in der Praxis oft einfach auf die Kontrolle der Konvergenzbedingung ganz verzichtet oder zumindest nur beim Startwert durchführt.
Geometrisch anschaulich bedeutet die Konvergenzbedingung, dass ein Startwert gut geeignet ist, wenn der Funktionswert 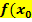 ) bereits nahe bei 0 liegt, der Graph an dieser Stelle wenig gekrümmt und ziemlich steil ist.
) bereits nahe bei 0 liegt, der Graph an dieser Stelle wenig gekrümmt und ziemlich steil ist.
Erläuterung:
Im Zähler der Konvergenzbedingung stehen die Ausdrücke  und
und 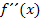 , im Nenner steht
, im Nenner steht 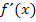 . Damit der gesamte Ausdruck
. Damit der gesamte Ausdruck 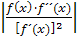 kleiner als 1 ist, muss der Zähler vom Betrag her kleiner als der Nenner sein. Ein Bruch ist schließlich immer kleiner als 1, wenn der Zähler kleiner als der Nenner ist. Der Zähler
kleiner als 1 ist, muss der Zähler vom Betrag her kleiner als der Nenner sein. Ein Bruch ist schließlich immer kleiner als 1, wenn der Zähler kleiner als der Nenner ist. Der Zähler 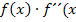 ) muss somit vom Betrag her klein und der Nenner
) muss somit vom Betrag her klein und der Nenner 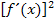 vom Betrag her großsein.
vom Betrag her großsein.
Der Zähler von 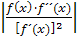 wird klein, wenn
wird klein, wenn  und
und 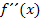 beide klein sind. Der Nenner wird groß, wenn
beide klein sind. Der Nenner wird groß, wenn 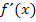 großist. Was bedeutet dies anschaulich?
großist. Was bedeutet dies anschaulich?
· Die erste Ableitung 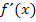 beschreibt bekanntlich die Steigung von
beschreibt bekanntlich die Steigung von 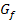 . Damit die Steigung
. Damit die Steigung 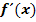 betragsmäßig groß wird, muss der Graph möglichst steil verlaufen.
betragsmäßig groß wird, muss der Graph möglichst steil verlaufen.
· Damit der Funktionswert 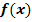 vom Betrag her klein, also fast 0 wird, muss x ganz in der Nähe der Nullstelle liegen.
vom Betrag her klein, also fast 0 wird, muss x ganz in der Nähe der Nullstelle liegen.
· Die zweite Ableitung f´´(x)beschreibt die Krümmung von 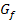 . Damit die Krümmung
. Damit die Krümmung 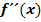 betragsmäßig klein wird, darf der Graph
betragsmäßig klein wird, darf der Graph 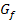 nicht allzu sehr gekrümmt sein. (D.h. er sollte beim Startwert keine zu enge Kurve beschreiben.)
nicht allzu sehr gekrümmt sein. (D.h. er sollte beim Startwert keine zu enge Kurve beschreiben.)
Ein Startwert  ist dementsprechend besonders gut geeignet, wenn gilt: ist dementsprechend besonders gut geeignet, wenn gilt:
|
Falls du momentan noch nicht gelernt hast, was die zweite Ableitung 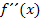 ist, kannst du die Formel der Konvergenzbedingung erst einmal vernachlässigen.
ist, kannst du die Formel der Konvergenzbedingung erst einmal vernachlässigen.

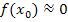 Das bedeutet, dass
Das bedeutet, dass 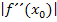 ist möglichst klein, was anschaulich einer geringen Krümmung an der Stelle
ist möglichst klein, was anschaulich einer geringen Krümmung an der Stelle 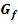 in der näheren Umgebung von
in der näheren Umgebung von 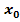 entspricht.
entspricht.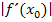 ist möglichst groß, was anschaulich bedeutet, dass
ist möglichst groß, was anschaulich bedeutet, dass 