Das Newton-Verfahren
Das Newton-Verfahren kann nicht nur bei Gleichungen der Form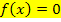 
verwendet werden, die sich vor allem bei der Nullstellenberechnung einer Funktion 
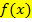ergeben, sondern auch bei Gleichungen der Form 
= 
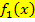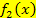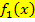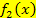, welche man bei der Schnittpunktberechnung zweier Funktionen und erhält. Solche Gleichungen müssen erst nach Null aufgelöst werden, bevor man das Newton-Verfahren anwenden kann.
= 
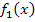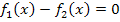
Der nun auf der linken Seite stehende Term entspricht der Funktion beim Newton-Verfahren. Somit gilt: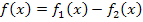 
Du hättest allerdings genauso gut die Gleichung =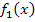 
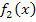zu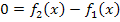 
umformen können. Dann hätte man 
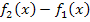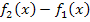als verwendet. Das würde ebenso zum richtigen Ergebnis führen. Falls dich das wundert, frage dich, wodurch sich die beiden Funktionen und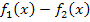 
unterscheiden. Das Vertauschen der Reihenfolge bei einer Differenz, dreht alle Vorzeichen um. Der Graph der Funktion 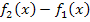ergibt sich aus dem Graphen der Funktion 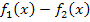durch Spiegelung an der x-Achse. Die Spiegelung an der x-Achse ändert jedoch nichts an den Schnittpunkten des Graphen mit der x-Achse. Daher haben die beiden Funktionen 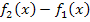und 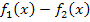die gleichen Nullstellen. Genau die Nullstellen von 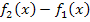bzw. 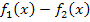wollen wir ja mit dem Newton-Verfahren berechnen. Daher ist es für das Ergebnis unerheblich, wie du die Gleichung 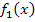= 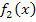nach Null auflöst. Du kannst somit alles auf die rechte Seite der Gleichung bringen oder auf die linke;Hauptsache es steht auf einer Seite des Gleichheitszeichen ausschließlich die Zahl Null. Das, was auf der anderen Seite der Gleichung steht, nimmst du als Funktion 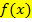für das Newton-Verfahren. Das Newton-Verfahren wendest du natürlich nur bei Gleichungen an, die sich nicht auf andere Weise exakt lösen lassen. Es liefert schließlich nicht die genaue Lösung, sondern nur einen Näherungswert. Wie gut die Näherung ist, hängt neben der Wahl des Startwertes wieder vor allem von der Anzahl der Rechenschritte ab, die vollzogen werden. Schauen wir uns doch sofort so eine Gleichung an und lösen sie mit dem Newton-Verfahren.
2. Bsp.:
Gegeben ist die Gleichung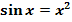 
. Ermittle mit dem Newton-Verfahren näherungsweise die positive Lösung der Gleichung auf drei Dezimalen genau!
Lösung:
Auf die Gleichung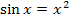 
kommt man, wenn man den Schnittpunkt der Funktionen 
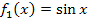und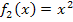 
berechnen soll. (Man muss dazu schließlich die beiden Funktionen gleichsetzen.) Wir sollen hier das Newton-Verfahren anwenden, um die Gleichung 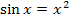zumindest näherungsweise zu lösen.
