Das Newton-Verfahren
Übersicht über die den Zwischenergebnissen zugewiesenen Buchstaben:
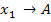
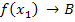
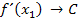
Berechnung von 
unter Verwendung der zwischengespeicherten Werte:
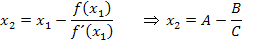
Tastenfolge zur Berechnung von :
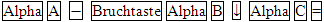
Du kannst natürlich auch direkt durch Einsetzen des ersten Näherungswertes in die komplette Formel, also in einem Schritt berechnen. Dabei kommt es aber bei vielen Schülern zu Tippfehlern;deshalb ist das nicht so zu empfehlen. Nur wenn du mit dem Speichern gar nicht klar kommst, gehst du nach dieser Methode vor:
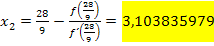(2. Näherungswert)
Der zweite Näherungswert 3,103835979 weicht vom ersten Näherungswert 3,111111111 bereits an der zweiten Nachkommastelle ab. Die gewünschte Genauigkeit von zwei Dezimalen ist offensichtlich noch nicht erreicht. Daher geht es gleich weiter mit der Berechnung des dritten Näherungswerts. Wir setzen den soeben berechneten zweiten Näherungswert wieder in die Iterationsvorschrift ein. Speichere dazu den Wert, den du für erhalten hast, vorweg am besten unter A ab. (Das bisher unter A gespeicherte Ergebnis von 
wird dann gelöscht;aber wir brauchen schließlich nicht mehr für die weitere Rechnung.)
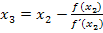
Die benötigten Zwischenergebnisse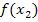 
und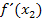 
speichern wir unter B und C im Taschenrechner. (Die dabei jeweils verwendeten Tastenfolgen entsprechen den bereits oben gezeigten Tastenfolgen bei der Berechnung des ersten Näherungswertes.) Dadurch werden natürlich die alten Belegungen mit 
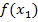bzw.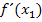 
gelöscht, aber diese Werte brauchen wir ja jetzt nicht mehr.
Übersicht über die neuen Belegungen der Speicher:
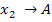
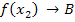
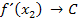
Berechnung von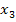 
unter Verwendung der zwischengespeicherten Werte:
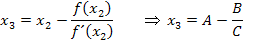
Du kannst 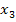natürlich auch wieder direkt durch Einsetzen des zweiten Näherungswertes 3,103835979 in die komplette Formel, also gleich in einem Schritt berechnen:
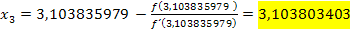(3. Näherungswert)
Die Lösung soll laut Angabe auf zwei Dezimalen genau angegeben werden. Da der dritte Näherungswert 3,103803403 vom zweiten Näherungswert 3,103835979 erst in der fünften Nachkommastelle abweicht, können wir hier sicher sagen, dass die Lösung 3,1038… lautet. Den vierten Näherungswert müssen wir also erfreulicherweise nicht mehr berechnen. Auf zwei Dezimalen gerundet lautet die gesuchte Lösung:
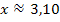
Damit ist diese Aufgabe gelöst! Die Gleichung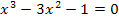 
hat somit näherungsweise die Lösung x = 3,10. Anschaulich bedeutet dies, dass die Funktion 
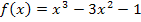ungefähr bei x = 3,10 ihre einzige Nullstelle hat.
Gleichungen der Form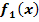 
= 
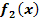mit dem Newton-Verfahren lösen:
