Das Newton-Verfahren
Alle weiteren Näherungswerte werden dann entsprechend berechnet. Die auf diese Art und Weise ermittelten Werte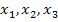 
usw. bilden zusammen eine Folge von Zahlen, die sich im günstigen Fall mit zunehmendem Index n immer näher an die exakte Lösung x = a der Gleichung 
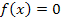annähern. Man sagt dann, die Werte 
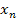konvergieren gegen die gesuchte Lösung a. Leider liefert das Newton-Verfahren nicht in jedem Fall Werte, die sich immer besser an die exakte Lösung a annähern. Das hängt nämlich von der Wahl des Startwertes ab.
Beginnt man die Rechnung mit einem ungeeigneten Startwert, kann dies dazu führen, dass die Werte 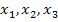sich mit zunehmendem Index immer weiter von a entfernen. Absolut ungünstig ist auch ein Startwert, wo die Tangente an 
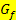waagrecht verläuft. Diese Tangente kann die x-Achse natürlich nicht schneiden. Es ergibt sich somit gar kein 
. Das merkt man auch an der Formel. Verläuft die Tangente bei 
waagrecht, gilt für die Ableitung an dieser Stelle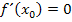 
. Da in der Formel 
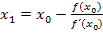der Ausdruck 
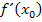im Nenner steht, darf 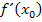aber nicht gleich Null sein, denn die Division durch Null ist ja nicht definiert. Es ist also entscheidend einen „guten“ Startwert zu verwenden;sonst liefert das Newton-Verfahren keine sinnvollen Näherungswerte für die exakte Lösung a. Bevor wir uns mit den Kriterien für einen geeigneten Startwert genauer befassen, wollen wir uns jedoch erst einmal ein paar konkrete Beispiele für Berechnungen mit dem Newton-Verfahren anschauen.
1. Bsp.:
Gegeben ist die Gleichung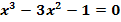 
. Ermittle mit dem Newton-Verfahren näherungsweise die Lösung der Gleichung auf zwei Dezimalen genau!
Lösung:
Da in der Aufgabenstellung kein Startwert angegeben ist, müssen wir selbst einen geeigneten Wert wählen. Der Startwert muss auf jeden Fall in der Nähe der gesuchten Lösung der Gleichung liegen. Die Gleichung ist bereits nach Null aufgelöst;sie liegt somit in der Form 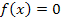vor. Die linke Seite der Gleichung stellen wir uns als Funktion 
vor. In diesem Beispiel gilt:
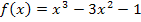
Mit Hilfe einer Wertetabelle kann der Graph der Funktion skizziert werden. Vergleiche dazu die folgende Wertetabelle und die Abbildung unten!
| x | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
|
-1,875 | -1 | -1,625 | -3 | -4,375 | -5 | -4,125 | -1 | 5,125 | 15 |
Hinweis:An Stelle der Wertetabelle kannst du auch mit Hilfe der relativen Extrema den Graph von schnell skizzieren. Wenn du diese Rechnung gerne sehen möchtest, gehe zu:Ausführliche Berechnung der Extrema zum 1. Bsp. (Newton-Verfahren) Am Verlauf von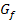 
erkennt man, dass die Funktion f(x) genau eine Nullstelle hat.
