Einige hilfreiche Informationen zum Thema „Anzahl gemeinsamer Punkte zweier Funktionen“
Du weißt bestimmt:Will man die Koordinaten von gemeinsamen Punkten zweier Funktionen berechnen, muss man die beiden Funktionen gleichsetzen. Auch um die Anzahl gemeinsamer Punkte zweier Funktionen zu bestimmen, muss man die Funktionen erst mal gleichsetzen. Die entstehende Gleichung muss jedoch nicht unbedingt komplett nach x aufgelöst werden, wenn es nur um die Anzahl der Lösungen geht. Die Anzahl der Lösungen einer Gleichung hängt von den folgenden Faktoren ab:
Wievielten Grades ist die Gleichung? Der Grad einer Gleichung ergibt sich aus der höchsten auftretenden Potenz von x. Eine Gleichung n.ten Grades hat maximal n verschiedene Lösungen. So hat zum Beispiel eine Gleichung dritten Grades, also eine Gleichung mit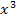 
als höchster Potenz, maximal 3 verschiedene Lösungen. Eine quadratische Gleichung, also eine Gleichung mit 
als höchster Potenz, besitzt dagegen nur höchstens 2 verschiedene Lösungen.
Tritt bei den Lösungen der Parameter unter einer Wurzel auf? Aus negativen Zahlen lässt sich die Wurzel bekanntlich überhaupt nicht ziehen. Deshalb gibt es gar keine Lösung, wenn der Ausdruck unter der Wurzel, der sogenannte Radikand, negativ wird. Ist der Radikand gleich Null, fallen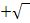 
und 
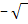zu einer einzigen (doppelten) Lösung zusammen, denn es gilt schließlich: 
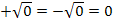Genau eine Lösung ergibt sich demnach aus 
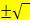, wenn der Ausdruck unter der Wurzel gleich Null wird. Zwei verschiedene Lösungen ergeben sich aus 
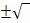, wenn der Radikand/Ausdruck unter der Wurzel positiv ist.
Können eine oder mehrere Lösungen für bestimmte Werte des Parameters zusammenfallen? Enthalten eine oder mehrere Lösungen den Parameter, können für bestimmte Werte des Parameters eventuell mehrere Lösungen zu einer einzigen zusammenfallen. Wenn man zum Beispiel die Lösungen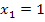 
und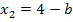 
erhalten hätte, ergäbe sich bei 
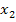für b = 3 die gleiche Lösung wie bei 
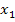. (Mit b = 3 ergibt sich schließlich: 
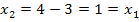) Für b = 3 würden die beiden Lösungen 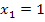und 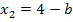zu einer einzigen Lösung 
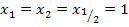zusammenfallen. Für b = 3 würde dann nur eine Lösung existieren;für alle anderen Werte von b erhielte man zwei verschiedene Lösungen. (Anmerkung:Die soeben erwähnten Lösungen 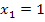und 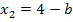haben nichts mit der Teilaufgabe 6c. zu tun;es handelt sich dabei nur um ein willkürlich gewähltes Beispiel, an dem die generelle Problematik erklärt werden sollte.)
