Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

Jetzt fehlt nur noch die zugehörige y-Koordinate. Wir erhalten sie, indem wir die berechnete x-Koordinate 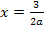in die Gleichung der Schar 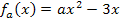für x einsetzen.

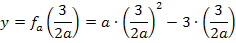
Dieses Ergebnis der y-Koordinate muss natürlich noch vereinfacht werden. Wir rechnen das Ganze daher so weit möglich aus. Wir quadrieren dazu den vorderen Bruch (einfach Zähler und Nenner einzeln zum Quadrat nehmen!) und multiplizieren den hinteren Bruch mit der Zahl 3, die davor steht. Die Zahl 3 eigentlich nur mit dem Zähler des Bruchs multiplizieren! Denn es gilt schließlich: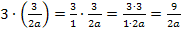

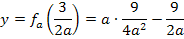
Nun lässt sich beim vorderen Bruch mit a kürzen. Das ergibt:

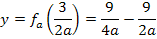
Um die beiden Brüche voneinander abziehen zu können, müssen beide Brüche auf den gleichen Nenner, d.h. den Hauptnenner, gebracht werden. Der Hauptnenner ist hier offensichtlich 4a , daher müssen wir den hinteren Bruch mit 2 Erweitern. 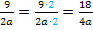Nachher lassen sich die beiden Brüche leicht voneinander subtrahieren.

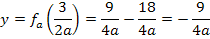
Dies ist die gesuchte y-Koordinate des Punktes mit waagrechter Tangente / des Scheitelpunktes.

Für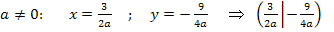

Für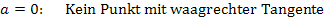

Damit ist diese Aufgabe gelöst.

Aufgaben mit Funktionenscharen sind bei Lehrer sehr beliebt, den meisten Schülern sind solche Aufgaben dagegen eher ein Graus. Aber sie kommen eben oft in Prüfungen dran und sind deshalb extrem wichtig.

Häufig finden sich in diesem Zusammenhang auch Aufgaben, in denen nach einer sogenannten Ortskurve bzw. Ortslinie oder dem geometrischen Ort bestimmter Punkte der Schar gefragt ist. Was ist damit gemeint?

Was ist zum Beispiel die Ortskurve der Hochpunkte? Das ist genau die Kurve, auf der alle Hochpunkte einer bestimmten Schar liegen. Anders formuliert:Würde man für unendlich viele verschiedene Werte des Parameters jeweils den Hochpunkt berechnen und all diese Hochpunkte in ein Koordinatensystem einzeichnen, erhielte man die Ortskurve der Hochpunkte.

Die Ortskurve der Tiefpunkte ist entsprechend die Kurve, auf der alle Tiefpunkte einer bestimmten Schar liegen.

Die Ortskurve der Wendepunkte ist dann logischerweise die Kurve, auf der alle Wendepunkte einer Schar liegen.

Damit du dir das Ganze besser vorstellen kannst, schauen wir uns gleich ein konkretes Beispiel dafür an.

Einführungsbeispiel zum Thema „Ortskurve“:

Wir betrachten die Funktionenschar 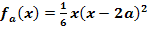mit a >0.

a.) Ermittle die Ortskurve der relativen Hochpunkte der Schar 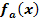! (In anderen Worten:Es ist die Gleichung derjenigen Kurve gesucht, auf der alle relativen Hochpunkte der Schar liegen.)

b.) Ermittle die Gleichung der Funktion, auf der alle Wendepunkte der Schar 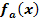liegen! (D.

---