Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Keine Parabel der Schar hat somit eine doppelte Nullstelle. Die Nullstelle 
ist sogar unabhängig von a. Das bedeutet, dass alle Graphen der Schar diese Nullstelle besitzen. Egal, was man für a einsetzt, die eine Nullstelle liegt immer bei . Der Ursprung (0|0) liegt also auf allen Graphen der Schar. Der Punkt (0|0) ist somit gemeinsamer Punkt aller Graphen der Schar.
Nun ist noch die Frage zu beantworten, für welchen Wert von a eine der Nullstellen bei x = -1 liegt. Die erste Nullstelle liegt für alle a bei . Nur die zweite Nullstelle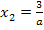 
ist von a abhängig und kann überhaupt bei x = -1 liegen. Es ist also die Frage zu klären, für welches a die Nullstelle 
gleich -1 ist.
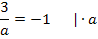
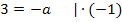
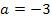
Nur für a = -3 ergibt sich demnach eine Nullstelle bei x = -1.
Zu 3d.)
Gesucht ist der Kurvenpunkt von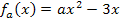 
, in dem die Tangente an 
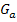waagrecht verläuft. Wenn die Tangente an 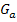waagrecht verläuft, muss ihre Steigung gleich Null sein. Weil die erste Ableitung 
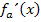der Tangentensteigung von 
entspricht, muss gelten:
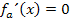
Wir bilden deshalb die erste Ableitung und setzen sie anschließend gleich Null.
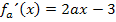
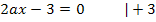
Vorsicht:Man kann nicht durch Null dividieren! Der Nenner ist hier jedoch von a abhängig, d.h. es kommt a im Nenner vor. Du musst dir daher überlegen, ob es einen Wert von a gibt, für den der Nenner gleich Null werden würde. Genau diesen Wert muss man dann nämlich ausschließen. Wenn der Nenner des Bruchs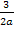 
Null wird, gibt es gar keinen Kurvenpunkt mit waagrechter Tangente, weil dann der Bruch 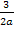überhaupt nicht definiert ist und andere Lösungen der Gleichung 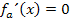gibt es nicht! Für welches a tritt diese Problematik auf? Richtig, bei a = 0. Für a = 0 würde der Nenner gleich Null werden und es gibt keinen Punkt mit waagrechter Tangente. Damit ist bereits der zweite Teil der Fragestellung beantwortet:Für a = 0 gibt es keinen Punkt mit waagrechter Tangente. Das leuchtet dir bestimmt ein, denn für a = 0 ergibt sich schließlich die einzige Gerade der Schar 
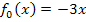und eine fallende Gerade kann schließlich keinen Punkt mit waagrechter Tangente haben.
Daher existiert ausschließlich für 
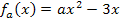ein Punkt mit waagrechter Tangente. Für sind die Graphen von Parabeln. Im Scheitelpunkt der jeweiligen Parabel verläuft die Tangente an den Graphen grundsätzlich waagrecht. Daher gibt es bei jeder Parabel, also für , einen Punkt mit waagrechter Tangente, eben den Scheitel dieser Scharparabel. Der Scheitelpunkt hat somit die x-Koordinate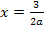 
.
