Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Wie lässt sich diese Gleichung am geschicktesten nach x auflösen? Die Gleichung enthält 
und x (ohne Potenz);sie ist also gemischtquadratisch. Du könntest sie deshalb mit der Lösungsformel für gemischtquadratische Gleichungen, der sogenannten Mitternachtsformel lösen;das ist aber viel zu umständlich. Weil in dieser Gleichung die Konstante c (d.h. die Zahl ganz ohne x) fehlt, lässt sich x nämlich einfach ausklammern. Dadurch entsteht eine Gleichung der Form „Produkt gleich Null“, welche sich ganz leicht lösen lässt:Man setzt einfach die Faktoren des Produkts einzeln gleich Null und löst jeweils nach x auf. Das kannst du bestimmt alleine. Also los geht´s!
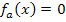
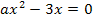
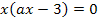
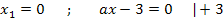
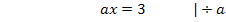
Wie viele Nullstellen gibt es hier? Was denkst du?
Wenn du glaubst, dass es hier immer zwei verschiedene Nullstellen gibt, weil schließlich zwei verschiedene Lösungen herausgekommen sind, hast du etwas Entscheidendes übersehen. Es gibt hier nicht immer zwei Nullstellen, denn für a = 0 ist die zweite Lösung gar nicht definiert. Dann gibt es nur die erste Lösung!
Vorsicht:Durch a dividieren darf man nur für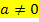 
! Daraus folgt, dass die zweite Nullstelle ausschließlich für 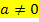existiert. Für a = 0 gibt es nur die erste Nullstelle 
.
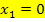Für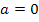 
: 1 einfache Nullstelle bei 
Für 
: 2 jeweils einfache Nullstellen bei und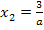 
Das macht auch Sinn, denn für a = 0 ergibt sich aus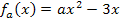 
die Funktion 
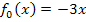, deren Graph 
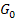eine Gerade ist, und eine Gerade kann die x-Achse schließlich nur einmal schneiden. Da der y-Achsenabschnitt der Gerade 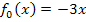offensichtlich t = 0 ist, handelt es sich bei 
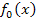um eine Gerade durch den Ursprung. Daher muss die einzige Nullstelle von 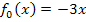zwangsläufig bei x = 0 liegen.
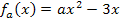Für sind die Graphen von dagegen Parabeln. Sie besitzen alle jeweils zwei verschiedene Nullstellen bei und 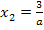. Alle Parabeln, die zu der Schar 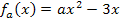gehören, schneiden die x-Achse an zwei verschiedenen Stellen, haben also alle jeweils zwei einfache Nullstellen. Das liegt daran, dass sich für immer zwei verschiedene Lösungen und 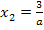ergeben. Weil die zweite Nullstelle 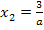niemals den Wert Null annehmen kann, fällt sie niemals mit der ersten Nullstelle zusammen. Zur Erinnerung:Ein Bruch wird nur dann gleich Null, wenn der Zähler gleich Null wird. (Null durch irgendwas ergibt immer Null.) Im Zähler von 
steht aber die Zahl 3 und die Zahl 3 kann schließlich niemals gleich Null sein. Daher kann der Bruch für keinen Wert von a gleich Null werden. Die Nullstellen und 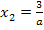fallen also für keinen Wert von a zusammen.
