Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Dabei ändert sich die Krümmung des Graphen natürlich genau im Wendepunkt.)
Du kannst die Gerade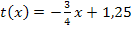 
entweder mit Hilfe ihres y-Achsenabschnittes t = 1,25 und ihrer Steigung 
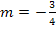zeichnen (auf der y-Achse 1,25 nach oben gehen, da ist der Schnittpunkt der Gerade mit der y-Achse. Von dort ein Steigungsdreieck zeichnen:4 nach rechts und 3 nach unten) oder einfach vom Wendepunkt W(1| 0,5) ausgehend das Steigungsdreieck zeichnen.
Die Extrema von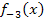 
kennen wir noch nicht. Aber die Extrema der Schar 
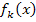haben wir in Teilaufgabe 9c.) bereits in Abhängigkeit von k ermittelt. Hier noch einmal die Ergebnisse von oben:
Wir müssen nur k = -3 in die Koordinaten des HOP bzw. TIP einsetzen und schon erhalten wir die Extrema von .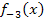
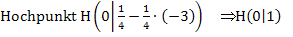
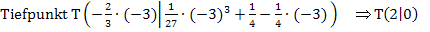
Mit den Nullstellen, den Extrema und dem Wendepunkt samt Wendetangente lässt sich der Graph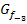 
leicht skizzieren. Du kannst natürlich auch eine Wertetabelle machen und damit den Graph zeichnen.
Hinweis nur für Schüler einer FOS zum Zeichnen des Graphs (nicht relevant für Gymnasiasten)
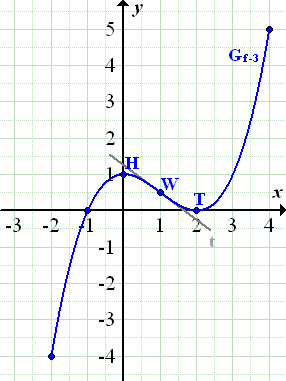
Abb.:Graph der Funktion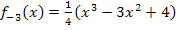 
im Intervall 
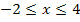zusammen mit der Wendetangente 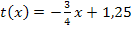, markiert sind die Randpunkte (-2| -4) und (4| 5), sowie die Extrempunkte H(0| 1) und T(2| 0), der Wendepunkt W(1| 0,5) und die Schnittpunkte mit der x-Achse (-1| 0) und (2| 0). (Der zweite Schnittpunkt mit der x-Achse entspricht dabei dem Tiefpunkt T.)
Zu 9g.)
Zur ersten Frage:Wie muss der Funktionsterm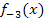 
verändert werden, damit an der Stelle x = 2 ein Hochpunkt entsteht? Dafür gibt es mehrere Möglichkeiten. In der vorherigen Teilaufgabe wurde der Graph von 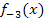gezeichnet. Du weißt also, dass 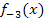bei x = 2 einen Tiefpunkt hat. Man kann deshalb den Graph von 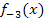einfach an der x-Achse spiegeln und schon hat man einen Graph, der bei x = 2 einen Hochpunkt hat. Setzt man vor den Funktionsterm von 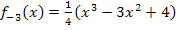ein Minuszeichen, erhält man eine an der x-Achse gespiegelte Funktion. Wir nennen diese Funktion hier 
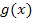. Eine mögliche Lösung ist demnach: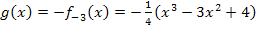 
Man kann den Graph der Funktion 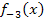aber auch um 2 nach rechts verschieben, denn 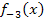hat ihren Hochpunkt bei H(0| 1). Durch die Verschiebung um zwei nach rechts, kommt der Hochpunkt bei (2| 1) zu liegen. Der Graph von 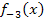verschiebt sich um 2 nach rechts, wenn man im Funktionsterm 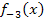jedes x durch (x – 2) ersetzt. Die um zwei nach rechts verschobene Funktion bezeichnen wir hier mit 
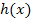. Eine weitere mögliche Lösung ist demnach: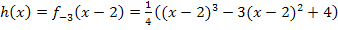 
Zur zweiten Frage:Wie muss der Funktionsterm 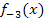verändert werden, damit im Ursprung ein Hochpunkt entsteht? Die Funktion 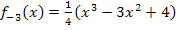hat bei H(0| 1) einen Hochpunkt.
