Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

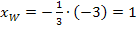
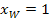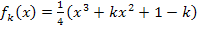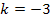Die y-Koordinate des Wendepunktes bekommen wir, indem wir in die Funktionsgleichung mit einsetzen, also in .

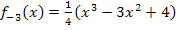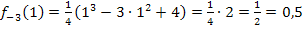
Der Wendepunkt für k = -3 hat somit die Koordinaten:W(1| 0,5)

Zu 9e.)

Gesucht sind alle Nullstellen der Funktion 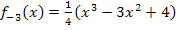einschließlich ihrer Vielfachheiten. Wir setzen daher die Funktion 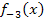gleich Null.

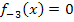
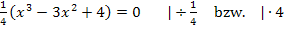
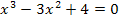
Es handelt sich bei der vorliegenden Gleichung um eine Gleichung dritten Grades, weil 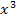die höchste auftretende x-Potenz ist. Wegen der Zahl 4 lässt sich leider x nicht einfach ausklammern. Wir müssen daher eine Polynomdivision machen. Normalerweise muss dazu die erste Lösung der Gleichung erraten werden;das ist hier jedoch unnötig, denn die erste Nullstelle 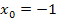ist uns aus Teilaufgabe 9a.) bekannt. Dort haben wir schließlich gezeigt, dass bei 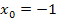jede Funktion der Schar 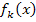eine Nullstelle besitzt. Also muss auch 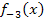dort eine Nullstelle haben.

Erste Nullstelle (schon bekannt):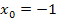

Polynomdivision:

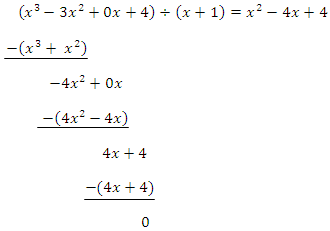
Das Ergebnis der Polynomdivision wird wieder gleich Null gesetzt.

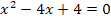
Diese Gleichung kann nun entweder mit der Mitternachtsformeloder mit der zweiten binomischen Formel gelöst werden.

1. Methode:Mit der Mitternachtsformel

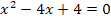
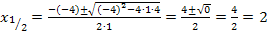
Weil die Diskriminante (d.h. der Ausdruck unter der Wurzel bei der Mitternachtsformel) hier gleich Null ist, ergibt sich eine doppelte Lösung. Die Lösungen 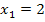und 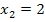fallen quasi zu einer einzigen (doppelten) Lösung 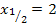zusammen.

2. Methode:Mit der zweiten binomischen Formel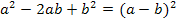

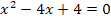
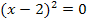
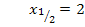
An dem Quadrat bei erkennt man, dass es sich bei x = 2 um eine doppelte Lösung handelt.

Bei 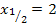handelt sich also um eine doppelte Nullstelle. Der Graph berührt dort die x-Achse. (Näheres dazu auch bei:Vielfachheiten der Nullstellen) Bei der bereits bekannten Nullstelle 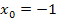handelt es sich um eine einfache Nullstelle;der Graph schneidet dort die x-Achse.

Zu 9f.)

Es soll der Graph 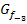der Funktion 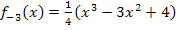und die Gerade 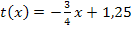im Intervall 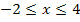in ein gemeinsames Koordinatensystem gezeichnet werden.

Aus den vorherigen Teilaufgaben ist bereits bekannt:

Nullstellen von 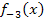: 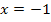(einfache Nst.) und 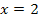(doppelte Nst.)

Wendepunkt von 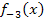:W(1| 0,5)

Außerdem wissen wir, dass die Gerade 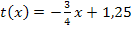die Wendetangente von 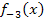ist. Die Gerade 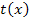solltest du einzeichnen, bevor du den Graph 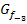skizzierst. (Man kann 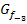nämlich viel genauer zeichnen, wenn man vorher schon die Wendetangente gezeichnet hat. Der Graph 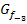schmiegt sich von der einen Seite an die Wendetangente an, schneidet sie genau im Wendepunkt und geht auf der anderen Seite wieder weg.

---