Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

Wo der Graph von 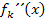unterhalb der x-Achse verläuft, ist 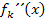negativ. Wo der Graph von 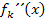oberhalb der x-Achse verläuft, ist 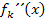positiv. So kommt man auch auf die Vorzeichen von 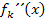, die man für die Krümmungstabelle benötigt.

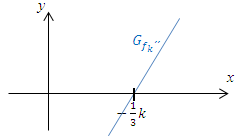
Abb.:Skizze des Graphen 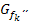der zweiten Ableitung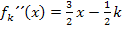

Zugehörige Krümmungstabelle für 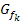mit Erklärung, wie man vom Verlauf des Graphen 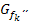der zweiten Ableitung auf die Vorzeichen von 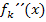und auf das Krümmungsverhalten von 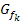kommt:

x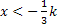
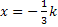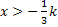Verlauf von	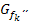(Gerade unterhalb x-Achse)	(Nst. der Gerade)	(Gerade oberhalb x-Achse)
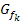	rechtsgekr.	WEP	linksgekr.

Nachweis des WEP:

2. Möglichkeit:Mit der dritten Ableitung (Nur für Schüler, die die dritte Ableitung auch im Unterricht behandelt haben.)

Damit an der Stelle 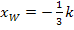ein Wendepunkt der Schar 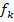liegt, muss die dritte Ableitung an dieser Stelle ungleich Null sein.

Hier noch einmal die zweite Ableitung:

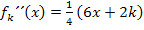
Wir bilden die dritte Ableitung:

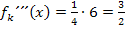
An sich muss jetzt die x-Koordinate 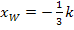für x in die dritte Ableitung eingesetzt werden;wir benötigen schließlich die dritte Ableitung an der Stelle .

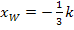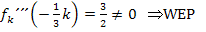
Weil hier aber gar kein x mehr in der dritten Ableitung vorkommt, ergibt sich auch an der Stelle 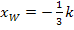für die dritte Ableitung der Wert 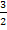, also ein Wert ungleich Null. Es handelt sich bei dem Punkt 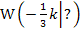also sicher um einen Wendepunkt der Schar.

Mit der x-Koordinate des Wendepunktes 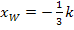lässt sich die Steigung m der zugehörigen Wendetangente in Abhängigkeit von k berechnen. Wir müssen dazu nur 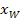in die erste Ableitung 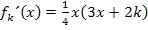einsetzen.

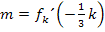
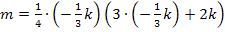
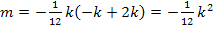
Der Parameter k soll so berechnet werden, dass die angegebene Gerade 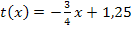Wendetangente von 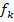ist. Die Steigung m muss dazu den Wert 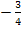annehmen.

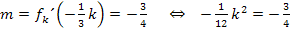
Da wir zeigen sollen, dass die Gerade 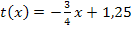für genau einen bestimmten Wert von k Wendetangente von 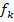ist, darf sich nur eine einzige Lösung aus dieser Gleichung ergeben. Dabei ist wieder zu beachten, dass k <0 gilt.

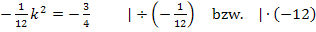
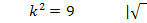
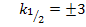
Wegen k <0 fällt die positive Lösung weg. Es gilt daher nur die Lösung k = -3, also genau eine Lösung. Nur für k = -3 ist die Gerade 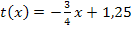Wendetangente von 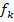. Es gibt also für k <0 wirklich nur einen Wert von k, für den die Gerade 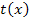Wendetangente der Schar ist. Genau das war zu beweisen.

Als letztes müssen wir noch die Koordinaten des Wendepunktes für k = -3 berechnen. In Abhängigkeit von k haben wir die x-Koordinate 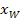des Wendepunktes vorher schon berechnet. Wir müssen nur noch k = -3 in 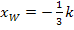einsetzen und schon haben wir die gesuchte x-Koordinate.

---