Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
)
Bei der Funktionenschar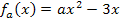 
mit a 
ℝhandelt es sich für 
um quadratische Funktionen, d.h. ihre Graphen sind Parabeln. Für positive Werte von a sind die Parabeln nach oben geöffnet;für negative Werte von a sind die Parabeln nach unten geöffnet. Für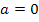 
liegt eine Gerade durch den Ursprung mit der Steigung -3 vor. Für a = 0 fällt 
nämlich komplett aus der Funktionsgleichung heraus: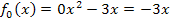 
Deshalb liegt für a = 0 keine quadratische Funktion / Parabel vor, sondern eine lineare Funktion / Gerade.
Für a >0:nach oben geöffnete Parabeln
Für a <0:nach unten geöffnete Parabeln
Für a = 0:fallende Gerade durch den Ursprung
Zu 3b.)
Es sollen die Graphen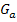 
der Schar 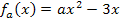für 
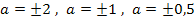und 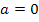in ein gemeinsames Koordinatensystem gezeichnet werden. Dazu setzen wir nacheinander die gegebenen Werte für a in die Gleichung 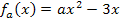ein.
Für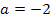 
ergibt sich die Gleichung: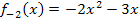 
Für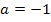 
ergibt sich die Gleichung: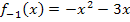 
Für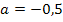 
ergibt sich die Gleichung: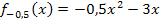 
Für 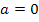ergibt sich die Gleichung: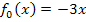 
Für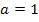 
ergibt sich die Gleichung: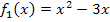 
Für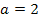 
ergibt sich die Gleichung: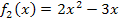 
Die Gerade 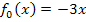kannst du leicht mit einem Steigungsdreieck zeichnen:Einfach vom Ursprung ausgehend 1 nach rechts und 3 nach unten gehen. Die Gerade hat schließlich die Steigung -3, also 
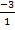. (Genaueres dazu bei:Geraden zeichnen) Die Parabeln kannst du zum Beispiel jeweils mit einer Wertetabelle zeichnen.
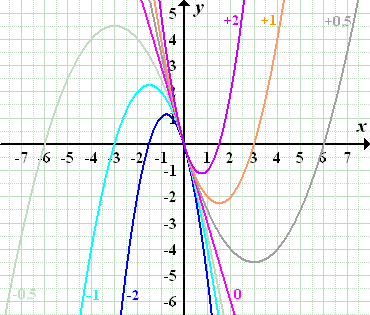
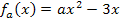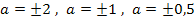Abb.:Die Graphen der Schar für und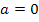
Zu 3c.)
Geg.: 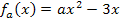mit a ℝ
Gesucht sind die Nullstellen der Schar in Abhängigkeit vom Parameter a. Dass man die Nullstellen einer Funktion berechnet, indem man den Funktionsterm gleich Null setzt, weißt du bestimmt. Doch was bedeutet der Zusatz „in Abhängigkeit von a“? Das bedeutet, dass du bei der Rechnung für a nichts Konkretes einsetzen darfst. Du musst einfach so tun, als wäre a eine bestimmte Zahl, z. B. 2 oder 3, aber du setzt diese Zahl nicht in die Funktionsgleichung 
ein. Du musst dir a also einfach als feste Zahl vorstellen, ohne jedoch etwas dafür einzusetzen. Der Parameter a wird in der gesamten Rechnung quasi mitgenommen.
Nullstellen der Schar in Abhängigkeit vom Parameter a berechnen:
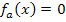
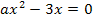
Nach was musst du jetzt auflösen? Nach x oder nach a?
Die Gleichung muss nach der Variablen, also nach x, aufgelöst werden, und nicht nach a. (a ist ja bloßder Parameter und stellt praktisch eine feste, wenn auch unbekannte Zahl dar.) Bei normalen Funktionen der Form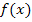 
löst man schließlich auch immer nach x auf, wenn man die Nullstellen berechnet.
