Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

Berechnung der x-Koordinate des Wendepunktes in Abhängigkeit von k:

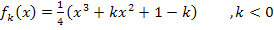
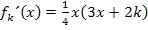
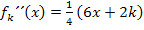
Notwendige Bedingung für WEP: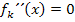

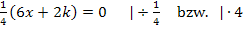
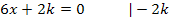
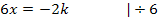
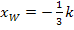
Nachweis des WEP:

(D.h. hinreichende Bedingung für WEP nachweisen)

1. Möglichkeit:Nachweis des Vorzeichenwechsels von 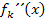an der Stelle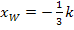

Wir erstellen dazu eine Krümmungstabelle.

x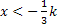

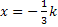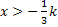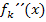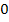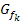Hier noch einmal die zweite Ableitung:

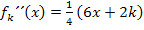
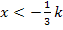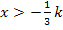Nun überlegen wir uns die Vorzeichen der zweiten Ableitung in den Bereichen und . Dabei ist zu beachten, dass k für eine negative Zahl steht, denn es gilt k <0. (Du musst dir folglich 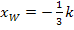als positive Zahl denken, obwohl ein Minus bei 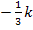vorkommt. 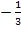mal eine negative Zahl wird schließlich positiv! Stell dir also vor, dass das Minuszeichen bei 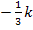gar nicht da wäre. Dann ist es nämlich leichter eine „Zahl“ zu finden, die kleiner bzw. größer ist als .)

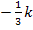Aus dem Intervall 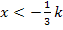nehmen wir beispielsweise die „Zahl“ 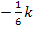. Wir setzen sie in die zweite Ableitung ein und bestimmen das Vorzeichen des Ergebnisses.

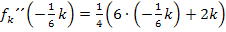
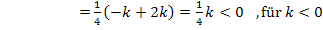
Aus dem Intervall 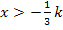nehmen wir beispielsweise die „Zahl“ 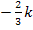. Wir setzen sie in die zweite Ableitung ein und bestimmen das Vorzeichen des Ergebnisses.

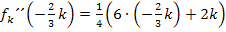
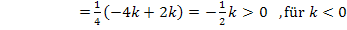
Wir tragen die Vorzeichen der zweiten Ableitung und das jeweilige Krümmungsverhalten von
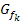an den entsprechenden Stellen der Tabelle ein.

x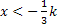
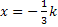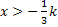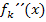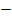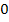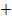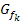	rechtsgekr.	WEP	linksgekr.

Auf Grund des Vorzeichenwechsels von 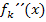an der Stelle 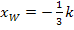liegt zwangsläufig ein Wendepunkt 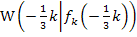der Scha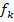r vor.

Hinweis:Wenn es dir schwer fällt, die Vorzeichen von 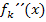durch Einsetzen bestimmter „Zahlen“ aus den jeweiligen Bereichen wie z. B. 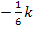und 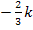zu bestimmen, kannst du die Vorzeichen von 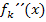auch graphisch ermitteln, indem du dir den Graph der zweiten Ableitung vorstellst. In diesem Fall geht das sehr leicht, denn der Graph von 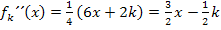ist für jedes beliebige k eine Gerade. Die Nullstelle dieser Gerade kennen wir schon, weil wir bei der Berechnung des Wendepunktes die Gleichung 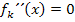schon gelöst haben. (Mit dem Ansatz 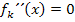haben wir schließlich die x-Koordinate 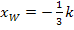des Wendepunktes von 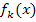berechnet. Mit 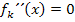berechnet man aber auch gleichzeitig die Nullstelle der zweiten Ableitung.) Die Nullstelle der Gerade 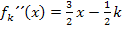liegt deshalb zwangsläufig bei 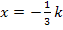. Dort schneidet die Gerade die x-Achse. Weil die Steigung der Geraden positiv ist, handelt es sich um eine steigende Gerade. (Vergleiche nachfolgende Skizze!) Links von 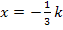, also für 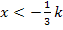verläuft die Gerade unterhalb der x-Achse und rechts davon, also für 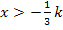oberhalb.

---