Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Wir müssen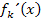 
also noch einmal ableiten, um 
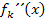zu erhalten. In die zweite Ableitung werden dann nacheinander die beiden berechneten x-Koordinaten 
und 
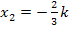eingesetzt. Ergibt sich ein negativer Wert, liegt ein Hochpunkt vor. Erhält man ein positives Ergebnis, handelt es sich um einen Tiefpunkt. Vergiss aber nicht, dass k hier für eine negative Zahl steht! Es gilt schließlich:k <0
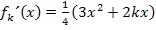
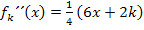
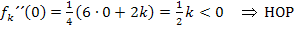
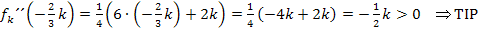
Die Extrempunkte lauten somit:
Außerdem ist nach der Kurve gefragt, auf der alle Tiefpunkte der Schar liegen, also nach der Ortskurve der Tiefpunkte. Weil wir die y-Koordinate des TIP bereits ausgerechnet haben, verwenden wir die 1. Methode zur Ermittlung der Ortskurve, d.h. x-Koordinate des TIP nach k auflösen und das Ergebnis in die y-Koordinate des TIP für jedes auftretende k einsetzen.
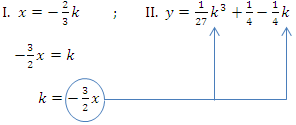
k in II.:
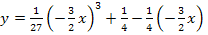
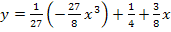
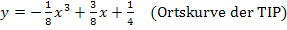
Als Letztes muss die Definitionsmenge für diese Ortskurve ermittelt werden. Die Variable x entspricht bei der Ortskurve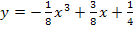 
den x-Koordinaten der Tiefpunkte. Wir müssen uns überlegen, welche Werte diese x-Koordinaten annehmen können. Wir wissen von oben, dass die Tiefpunkte der Schar 
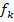die x-Koordinate 
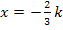haben. Wegen k <0 stellt der Parameter k eine negative Zahl dar; 
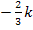ist dann eine positive Zahl. (Die negative Zahl 
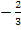multipliziert mit der negativen Zahl k ergibt schließlich etwas Positives.) Die x-Koordinate der TIP 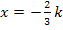ist also für k <0 immer positiv. Deshalb haben alle Tiefpunkte eine positive x-Koordinate;es gilt somit bei der Ortskurve der TIP:x >0
Oder anders formuliert:Die Definitionsmenge der Ortskurve ist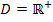 
.
Zu 9d.)
Es soll gezeigt werden, dass die Gerade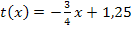 
für genau einen bestimmten Wert von k Wendetangente an den Graphen 
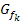ist. Außerdem ist nach den Koordinaten des Wendepunktes von 
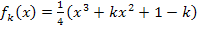für diesen Wert von k gefragt. Um diese Aufgabe zu lösen, muss zuerst die x-Koordinate 
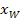des Wendepunktes der Schar in Abhängigkeit von k berechnet werden. Danach kann man die Steigung m der Wendetangente in Abhängigkeit von k ausrechnen, indem man die ermittelte x-Koordinate 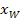des Wendepunktes in die erste Ableitung 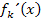einsetzt: 
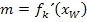Das Ergebnis setzt man dann mit der Steigung der angegebenen Gerade 
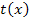gleich, also mit 
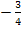. Aus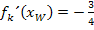 
erhält man eine Gleichung, die nur noch nach k aufgelöst werden muss. Dabei muss sich genau eine Lösung für k ergeben, weil schließlich gezeigt werden soll, dass die Gerade 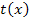für genau einen bestimmten Wert von k Wendetangente an den Graphen 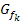ist.
