Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
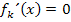
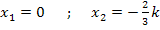
Berechnung der zugehörigen y-Koordinaten:
Wir setzen dazu die x-Koordinaten jeweils in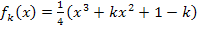 
ein.
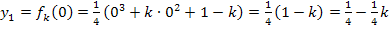
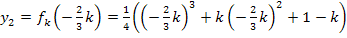
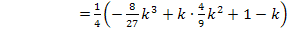
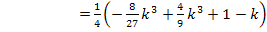
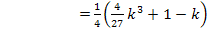
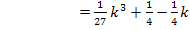
Nun kennen wir die Koordinaten der Punkte mit waagrechter Tangente:
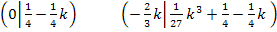
Art der Extrema untersuchen:
1. Möglichkeit:Monotonieuntersuchung
Wir erstellen eine Monotonietabelle. Beachte dabei, dass wegen k <0 die zweite x-Koordinate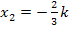 
positiv ist und somit 
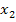größer ist als die erste x-Koordinate 
. Daher muss 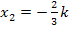in der Tabelle rechts von stehen.
| x |  |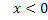
 |
 |
 |
 |
 |
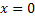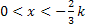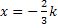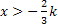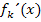0 | 0 | |||
 |
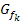Nun muss man sich die Vorzeichen der Ableitung in den drei Bereichen überlegen. Dazu verwenden wir die Ableitung in der faktorisierten Form (Produktform), also mit ausgeklammertem x.
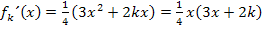
Wir beginnen mit dem Intervall x <0. Wenn x für eine negative Zahl steht, ist der erste Faktor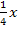 
auch negativ. Auch der zweite Faktor 
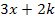ist dann sicher negativ, weil ja auch k negativ ist. Es ergibt sich: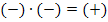 
Nun zum Intervall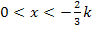 
. Wenn x in diesem Intervall liegt, steht x auf jeden Fall für eine positive Zahl. Der erste Faktor 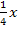ist dann auch positiv. Der zweite Faktor 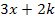ist dagegen negativ, weil x kleiner ist als 
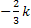und k für eine negative Zahl steht. Wenn dir das nicht ganz klar ist, setze doch einfach eine Zahl aus dem Intervall 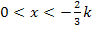, also zum Beispiel 
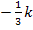in den zweiten Faktor 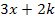ein: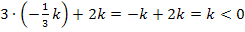 
, weil k hier schließlich für eine negative Zahl steht. Insgesamt ergibt sich in diesem Intervall für das Vorzeichen der Ableitung: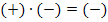 
Als letztes zum Intervall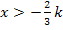 
. Wenn x in diesem Intervall liegt, stellt x auf jeden Fall eine positive Zahl dar. Der erste Faktor 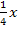ist dann auch wieder positiv. Der zweite Faktor 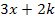ist ebenfalls positiv, weil x größer ist als 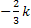und k für eine negative Zahl steht. Wenn dir das nicht ganz klar ist, setze doch einfach eine Zahl aus dem Intervall 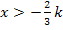, also zum Beispiel 
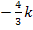in den zweiten Faktor 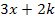ein: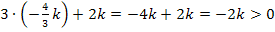 
,weil k hier schließlich für eine negative Zahl steht. Insgesamt ergibt sich in diesem Intervall für das Vorzeichen der Ableitung: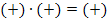 
Wen man die ermittelten Vorzeichen und das jeweilige Steigungsverhalten in die Tabelle einträgt, kommt man zu der folgenden Monotonietabelle:
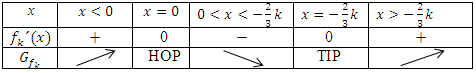
Es liegt bei und 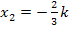jeweils ein Vorzeichenwechsel von 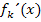vor;es handelt sich daher um Extrema. Bei liegt ein Hochpunkt der Schar und bei 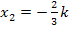ein Tiefpunkt. Die zugehörigen y-Koordinaten haben wir oben schon ausgerechnet. Die Extrempunkte lauten somit:
2. Möglichkeit:Mit der zweiten Ableitung
Die erste Ableitung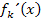 
haben wir schon vorher ermittelt.
