Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Zu 9b.)
Geg.: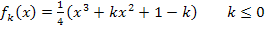 
Gesucht ist in Abhängigkeit von k die Anzahl der Punkte von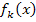 
, die eine waagrechte Tangente haben. Bei einer waagrechten Tangente ist die Steigung gleich Null. Deshalb muss bei einem Punkt mit waagrechter Tangente die erste Ableitung 
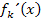gleich Null sein. Es muss dort gelten:
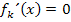
Die erste Ableitung haben wir in Teilaufgabe 9a.) bereits gebildet. Sie lautet:
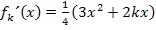
Wir setzen sie gleich Null und überlegen uns bei der entstehenden Gleichung die Anzahl der Lösungen.
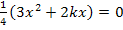
Diese Gleichung enthält 
und x (ohne Potenz);sie ist daher gemischtquadratisch. Gemischtquadratische Gleichungen können natürlich mit der Mitternachtsformel gelöst werden. Die Diskriminante würde dann über die Anzahl der Lösungen entscheiden. Das ist hier aber viel zu umständlich, denn es kommt keine Konstante c (d.h. Zahl ganz ohne x) in der Gleichung vor. Deshalb lässt sich auf der linken Seite der Gleichung x ausklammern. Dadurch ergibt sich eine Gleichung der Form „Produkt gleich Null“. Da ein Produkt bekanntlich gleich Null ist, wenn einer der Faktoren gleich Null ist, kann man dann die Faktoren einzeln gleich Null setzen.
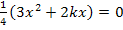
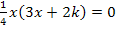
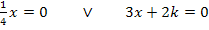
Es geht hier um die Anzahl der Lösungen. Die erste Lösung 
ist unabhängig von k, weil dabei kein k in der Lösung vorkommt. Diese Lösung gibt es auf jeden Fall. Alle Graphen der Schar haben somit bei einen Punkt mit waagrechter Tangente. Die zweite Lösung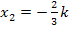 
ist dagegen von k abhängig;es kommt dabei schließlich ein k vor. Die Frage ist nun, ob 
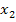mit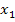 
zu einer einzigen (doppelten) Lösung zusammenfallen kann und wenn ja, für welchen Wert von k dies der Fall ist. Offensichtlich fallen die beiden Lösungen nur für k = 0 zusammen. Für alle anderen Werte von k ergeben sich jeweils zwei verschiedene Lösungen 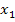und 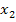. Da laut Angabe gilt 
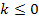gehört auch k = 0 zu den zulässigen Werten von k;wir müssen also eine Fallunterscheidung machen.
Anzahl der Punkte von 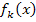mit waagrechter Tangente:
Für k = 0:1 Punkt mit waagrechter Tangente bei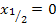 
Für k <0:2 Punkte mit waagrechter Tangente bei und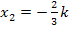
Zu 9c.)
Geg.: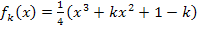 
Es gilt nun k <0. Gesucht ist die Art und Lage aller Extrempunkte der Schar in Abhängigkeit von k. Wir sollen also die Koordinaten aller Extrempunkte berechnen und entscheiden, ob es sich dabei um Hoch- oder Tiefpunkte handelt. Damit ein Extremum vorliegen kann, muss dort die Tangente an den Graph waagrecht verlaufen. Die x-Koordinaten der Punkte von 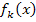mit waagrechter Tangente haben wir in Teilaufgabe 9b.) schon ausgerechnet.
