Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Egal, was man für k einsetzt, es ergibt sich bei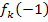 
immer das Ergebnis 0. D.h. unabhängig von k ist die Aussage 
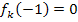wahr. Alle Graphen der Schar 
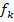haben daher bei 
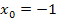eine Nullstelle. Genau das war als erstes zu zeigen.
2. Bei 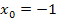wird die x-Achse von allen Graphen der Schar 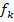geschnitten. Es muss daher gezeigt werden, dass für alle zulässigen Werte von k gilt: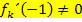 
Erläuterung:Wenn eine Funktion die x-Achse bei 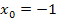schneidet, kann die x-Achse in diesem Punkt nicht Tangente an die Funktion sein. Nur wenn eine Funktion die x-Achse berührt, aber nicht schneidet, ist die x-Achse im Berührpunkt Tangente an die Funktion. Da die x-Achse waagrecht verläuft, wäre die x-Achse waagrechte Tangente an die Funktion, wenn dort ein Berührpunkt vorläge. Genau das ist in unserem Beispiel aber nicht der Fall. Die Funktion kann also bei 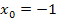keine waagrechte Tangente haben. Wir müssen deshalb zeigen, dass 
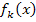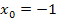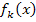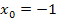für alle zulässigen Werte von k bei keine waagrechte Tangente hat. Die Steigung von bei darf demnach nicht gleich Null sein. Daraus folgt:Die erste Ableitung 
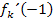darf nicht gleich Null sein, egal was für k eingesetzt wird.
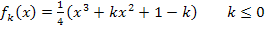
Wir bilden die erste Ableitung:
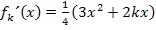
Um 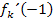zu bilden, setzen wir -1 für x in die Ableitung ein:
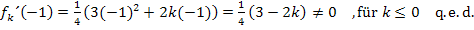
Da laut Angabe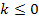 
gilt, ist das Ergebnis 
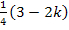für alle zulässigen Werte von k ungleich Null. Für alle negativen Werte von k und auch für k = 0 ist das Ergebnis sicher positiv, also ungleich Null. Warum? Für k = 0 kommt nämlich 
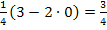heraus;das ist offensichtlich nicht gleich Null. Für negative Werte von k überlegt man sich Folgendes:Wenn k selbst negativ ist, ist – 2k etwas Positives. D.h. der Ausdruck 3 – 2k ist dann auch positiv, weil zu der positiven Zahl 3 noch etwas dazu addiert wird. Multipliziert man den positiven Ausdruck (3 – 2k) mit der positiven Zahl 
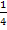, kommt natürlich wieder etwas Positives heraus. Deshalb gilt für k >0: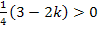 
Solange k positiv oder gleich Null ist, ergibt sich also bei 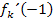ein Ergebnis ungleich Null. (Hierbei ist also die Angabe 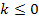entscheidend! Für 
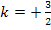würde der Ausdruck 
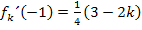nämlich doch gleich Null werden: 
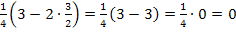Für 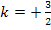wäre das Ergebnis gleich Null, aber positive Werte von k sind laut Angabe nicht zugelassen.) Die Steigung der Scharfunktionen an der Stelle 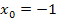ist daher für alle zulässigen Werte von k sicher nicht gleich Null. Die Tangente an 
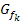verläuft bei 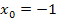somit für alle 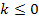bestimmt nicht waagrecht und die x-Achse kann daher an dieser Stelle nicht berührt werden. Alle Graphen der Schar schneiden folglich bei 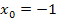die x-Achse. Genau dies war zu beweisen.
