Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
An der Beispielaufgabe 8 konntest du sehen, wofür man Funktionenscharen brauchen kann und woher die Gleichung einer Schar kommen kann. Es gibt natürlich noch unzählige weitere typische Anwendungsaufgaben von Scharen. Doch diese alle zu zeigen, würde den Rahmen dieser website sprengen. Die wichtigsten Aufgabentypen zum Thema Funktionenscharen haben wir nun besprochen. Abschließend noch ein kleiner Test, ob du auch alles verstanden hast. Die nächste Aufgabe solltest du wirklich alleine versuchen zu rechnen und erst nachher die Lösung zur Kontrolle anschauen. Die Aufgabe ist nicht ganz einfach. Wenn du sie aber selbständig richtig lösen kannst, bist du bestimmt fit für deine nächste Schulaufgabe zu diesem Thema.
9. Bsp.:Aus einer alten Schulaufgabe
Gegeben ist die Funktionenschar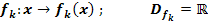 
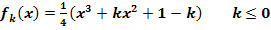
Der Graph einer solchen Funktion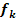 
in einem kartesischen Koordinatensystem wird mit 
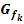bezeichnet.
a.) Zeige, dass alle Graphen 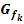der Schar 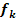an der Stelle 
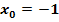eine gemeinsame Nullstelle besitzen und, dass alle Graphen 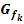die x-Achse an dieser Stelle schneiden.
b.) Ermittle die Anzahl der Punkte mit waagrechter Tangente einer Funktion der Schar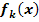 
in Abhängigkeit von k!
c.) Berechne für k <0 die Lage und Art aller Extrema der Schar 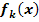in Abhängigkeit von k! Auf welcher Kurve liegen die Tiefpunkte der Schar?
d.) Zeige, dass die Gerade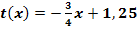 
für genau einen bestimmten Wert von k <0 Wendetangente an den Graphen 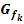ist. Welche Koordinaten hat der Wendepunkt für diesen Wert von k?
e.) Es sei nun k = -3. Gib alle Nullstellen der Funktion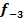 
einschließlich ihrer Vielfachheiten an!
f.) Zeichne den Graph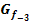 
und die Gerade 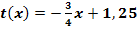in ein gemeinsames Koordinatensystem. (1 LE 
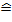1 cm;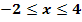 
)
g.) Wie muss der Funktionsterm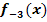 
verändert werden, damit an der Stelle x = 2 ein Hochpunkt entsteht? Wie muss der Funktionsterm 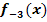verändert werden, damit im Ursprung ein Hochpunkt entsteht?
Lösung:
Zu 9a.)
Geg.: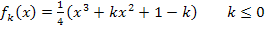 
Vorsicht:Der Parameter k steht hier für eine negative Zahl oder Null!
Es soll gezeigt werden, dass alle Graphen der Schar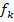 
an der Stelle 
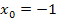eine gemeinsame Nullstelle besitzen und, dass sie alle die x-Achse an dieser Stelle schneiden und nicht etwa berühren. Es müssen also zwei Dinge nachgewiesen werden:
1. Bei 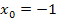liegt eine Nullstelle aller Graphen der Schar. Es muss daher gezeigt werden, dass für alle zulässigen Werte von k gilt: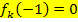 
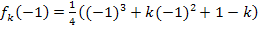
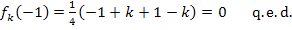
Hinweis:q.e.d. ist eine Abkürzung für „quod erat demonstrandum“ (Latein). Auf Deutsch heißt das „was zu zeigen war“.
