Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
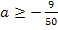
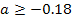
Für diese Werte von a wird eine Steigung von 1,5 nicht überschritten. Damit ist die Aufgabe gelöst.
Damit du dir das Ganze besser vorstellen kannst, hier noch eine Abbildung, in der drei ausgewählte Graphen der Schar 
zu sehen sind. Die Wendepunkte sind dabei rot markiert. Dort verlaufen die Graphen jeweils am steilsten. Außerdem sind die Wendetangenten (in derselben Farbe wie der zugehörige Graph) miteingezeichnet.
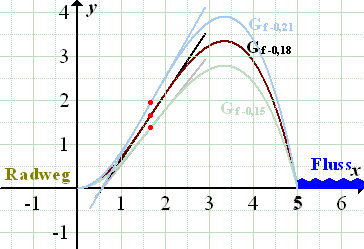
Abb.:Drei ausgewählte Graphen der Schar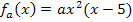 
mit ihren Wendetangenten. Dargestellt sind die Graphen zu a = -0,15 , a = -0,18 und a = -0,21 im Intervall x 
[0;5].
Nur für 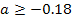ist die Bedingung erfüllt, dass der Damm auf seiner linken Seite eine Steigung von 1,5 nicht überschreitet. Das haben wir oben so ausgerechnet.
Der Graph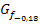 
zu a = -0,18 (schwarz dargestellt) stellt somit die Grenze dar zwischen den Graphen, die zu steil sind, und denen, die flach genug verlaufen, also eine Steigung von weniger als 1,5 haben. 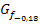ist der höchste Graph der Schar, der gerade noch die Bedingung erfüllt.
Alle Graphen, die zu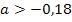 
gehören, liegen unterhalb des schwarz dargestellten 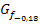. Auch sie erfüllen die Bedingung;sie sind nicht zu steil. Als Beispiel dafür ist in der Abbildung 
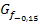zu a = -0,15 (grau) gezeigt.
Die Graphen für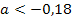 
liegen oberhalb des schwarz dargestellten 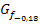. Diese Graphen sind zu steil. Als Beispiel für einen zu steilen Graph ist in der Abbildung 
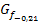zu a = -0,21 (in Blau) dargestellt.
Wenn Herr Müller sich nun für einen bestimmten Damm entscheiden möchte, wird er wohl denjenigen wählen, der zwar nicht zu steil ist, aber gleichzeitig auch möglichst hoch ist, damit der Damm auch bei sehr hohen Wasserständen des Flusses einen ausreichenden Schutz gegen Überflutungen gewährt. Er sollte also a = -0,18 wählen.
Die Funktion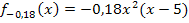 
würde also im Bereich x [0;5] den Querschnitt des optimalen Dammes beschreiben.
Hinweis:Die Wendepunkte der Schar haben alle dieselbe x-Koordinate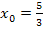 
;sie unterscheiden sich aber in ihrer y-Koordinate. Diese y-Koordinaten haben wir zwar nicht ausgerechnet, man kann der oben gezeigten Abbildung jedoch entnehmen, dass die y-Koordinaten der Wendepunkte der Schar von a abhängen. Für unterschiedliche Werte von a liegen die Wendepunkte in unterschiedlicher Höhe. Die x-Koordinate der WEP 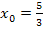ist dagegen unabhängig von a. Die Wendepunkte 
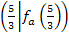der Schar liegen deshalb senkrecht übereinander auf der senkrechten Gerade 
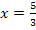. Diese senkrechte Gerade stellt somit die Ortskurve der Wendepunkte der Schar dar.
