Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Die Graphen der ersten Ableitung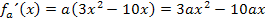 
mit a 
]-1;0[ sind alle nach unten geöffnete Parabeln, weil es sich bei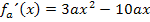 
um quadratische Funktionen mit negativem Öffnungsfaktor handelt. Der Öffnungsfaktor ist die Zahl bzw. der Ausdruck, der direkt vor 
steht, also in diesem Fall 3a.
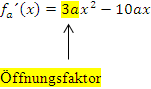
Wegen a ]-1;0[ steht a für eine negative Zahl und somit ist auch der Öffnungsfaktor 3a negativ. Wenn der Öffnungsfaktor negativ ist, ist die zugehörige Parabel nach unten geöffnet und der Scheitel der Parabel bildet das absolute Maximum der Parabel. Beim Scheitel von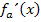 
verläuft die Tangente an den Graph der Ableitungsfunktion 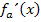waagrecht. Dort ist also die Steigung der ersten Ableitung 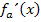, d.h. die zweite Ableitung 
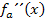, gleich Null. Die Gleichung 
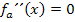haben wir oben bei der Berechnung des Wendepunktes von 
natürlich schon gelöst. So sind wir schließlich auf die x-Koordinate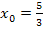 
gekommen. (An der Stelle, wo die Funktion ihren Wendepunkt hat, hat die erste Ableitungsfunktion 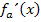ihr Extremum.) Der Scheitel der Ableitungsfunktion 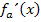muss deshalb zwangsläufig bei 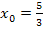liegen. Weil die Graphen von 
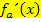nach unten geöffnete Parabeln mit Scheitel 
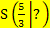sind, müssen die Ableitungsfunktionen 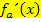bei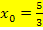 
ihr absolutes Maximum haben. Das bedeutet wiederum, dass die Steigung von 
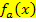bei 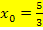maximal sein muss und dass die Graphen der Schar 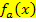dort am stärksten steigen. Die erste Ableitung 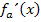entspricht schließlich der Steigung von .
Als letztes muss a so berechnet werden, dass der Damm auf der flussabgewandten Seite eine Steigung von 1,5 nicht überschreitet. Wir wissen inzwischen, dass der Damm an der Stelle 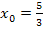seine größte Steigung besitzt;diese Stelle liegt auf der flussabgewandten/linken Seite, da 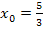kleiner ist als die x-Koordinate des Hochpunktes 
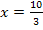. (Vergleiche Teilaufgabe 8b.) Damit der Damm auf der flussabgewandten Seite nicht steiler als 1,5 wird, darf seine Steigung an der steilsten, flussabgewandten Stelle nicht größer als 1,5 sein. Das bedeutet, dass der Damm, also die Funktion 
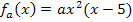, an der Stelle 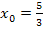nicht steiler als 1,5 sein darf. Die Steigung von 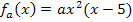bei 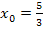entspricht der Ableitung 
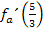;sie darf nicht größer sein als 1,5. Anders formuliert: 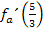soll kleiner oder gleich 1,5 sein. Es muss demnach gelten:
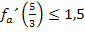
Hier noch einmal die erste Ableitung: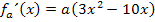 
Wir bilden 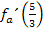, indem wir für x den Wert 
in die erste Ableitung einsetzen. Das Ergebnis setzen wir dann kleiner oder gleich 1,5.
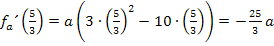
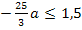
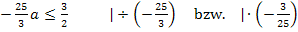
Vorsicht:Hier dreht sich das Ungleichheitszeichen laut Inversionsgesetz um, weil man mit einer negativen Zahl multipliziert bzw. durch eine negative Zahl dividiert!
