Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

Wir tragen die ermittelten Vorzeichen und das entsprechende Krümmungsverhalten (links- bzw. rechtsgekrümmt) in die Krümmungstabelle ein. Weil bei 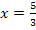ein Vorzeichenwechsel der zweiten Ableitung vorliegt, handelt es sich dabei wirklich um eine Wendestelle. Der Vorzeichenwechsel von 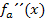ist bekanntlich eine hinreichende Bedingung für einen Wendepunkt. Würde sich das Vorzeichen der zweiten Ableitung nicht ändern, läge nur ein Flachpunkt/FLAP vor, aber eben kein Wendepunkt. Mehr dazu bei:Zweite Ableitung f´´(x)

x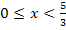
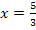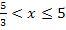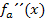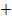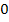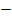	linksgekrümmt	WEP	rechtsgekrümmt

2. Methode:Nachweis des Wendepunktes mit der dritten Ableitung (nur für Schüler, die die dritte Ableitung im Unterricht behandelt haben)

Damit bei 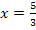tatsächlich ein Wendepunkt/WEP und nicht etwa bloßein Flachpunkt/FLAP vorliegt, muss die dritte Ableitung an dieser Stelle ungleich Null sein. (Siehe auch:Wendepunkte mit der dritten Ableitung nachweisen) Wir bilden daher die dritte Ableitung.

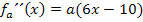
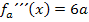
An sich müsste man jetzt für x die Zahl in die dritte Ableitung einsetzen. Nun kommt aber in diesem Fall in der dritten Ableitung gar kein x mehr vor. Das ist nicht weiter problematisch. Das bedeutet einfach, dass die dritte Ableitung an jeder Stelle x gleich 6a ist. Man muss also nicht wirklich für x die Zahl in die dritte Ableitung einsetzen. Es kommt sowieso immer das gleiche heraus, in unserem Fall 6a. Wegen 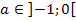kann a nicht gleich Null sein und deshalb ist die dritte Ableitung auf jeden Fall ungleich Null, auch an der Stelle 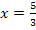. Es handelt sich also tatsächlich um einen Wendepunkt.

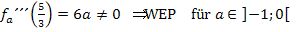
Anmerkung:Dass in der dritten Ableitung kein x mehr vorkommt, ist gar nichts Außergewöhnliches. Das ist bei allen Polynomfunktionen 3. (und niedrigeren) Grades so. Eine Polynomfunktion 3. Grades hat allgemein die Gleichung 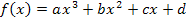mit . Beim Ableiten wird von den x-Potenzen jeweils 1 abgezogen, so dass die zweite Ableitung als höchste Potenz nur noch enthält. Die zweite Ableitung enthält entsprechend bloßnoch 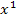, also x, als höchste Potenz. Bei der dritten Ableitung kommt dann logischerweise gar kein x mehr vor.

Egal mit welcher der beiden Methoden, auf jeden Fall haben wir gezeigt, dass alle Graphen der Schar 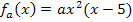mit a ]-1;0[ und x [0;5] unabhängig von a bei 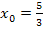eine Wendestelle besitzen. Es bleibt zu zeigen, dass die Graphen der Schar dort am stärksten steigen und nicht etwa am stärksten fallen. Anders formuliert:Es ist zu beweisen, dass bei 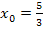die Steigung von maximal ist, also dass die erste Ableitung 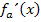dort ein absolutes Maximum hat.

---