Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

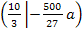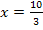Punkte, die sich nur in ihrer y-Koordinate, nicht aber in ihrer x-Koordinate unterscheiden, liegen zwangsläufig senkrecht übereinander. Die Hochpunkte der Schar liegen alle auf der senkrechten Gerade . Diese senkrechte Gerade stellt somit die Ortskurve der Hochpunkte der Schar dar.

Zu 8c.)

Geg.: 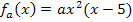mit a ]-1;0[ und x [0;5]

Es ist zu zeigen, dass alle Graphen der Schar unabhängig von a an der gleichen Stelle 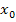am stärksten steigen. Im Prinzip bedeutet das, dass wir zeigen sollen, dass die x-Koordinate der Wendepunkte der Schar unabhängig ist von a. Der Wendepunkt einer Funktion ist nämlich derjenige Kurvenpunkt, wo der Graph der Funktion am steilsten (bzw. flachsten) verläuft, also wo der Graph entweder am stärksten steigt oder fällt (bzw. am wenigsten steigt oder fällt). In diesem Fall sind die Graphen im Wendepunkt am stärksten steigend, was man auch an der in Teilaufgabe 8a.) gezeigten Abbildung sehen kann. Wir müssen also die x-Koordinate des Wendepunkts berechnen. Dabei darf der Parameter a nicht mehr im Ergebnis vorkommen;nur dann ist das Ergebnis unabhängig vom Parameter a.

Um die x-Koordinate des Wendepunktes zu berechnen, brauchen wir die zweite Ableitung.

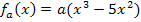
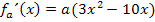
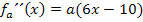
Berechnung der x-Koordinate des Wendepunktes:

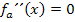
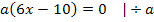
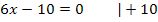
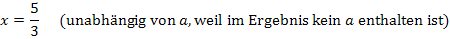
In der Aufgabenstellung wird diese Stelle mit bezeichnet. Daher gilt: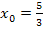

Nachweis, dass bei 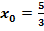tatsächlich ein Wendepunkt von 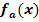vorliegt:

1. Methode:Nachweis des Vorzeichenwechsels von 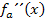bei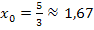

Wir fertigen dazu eine Krümmungstabelle für x [0;5] an.

x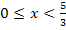

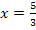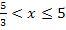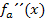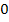Hier noch einmal die zweite Ableitung:

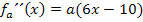mit a ]-1;0[ und x [0;5]

Wir müssen jetzt die Vorzeichen von 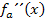in den Intervallen 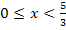und 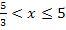ermitteln. Dazu wählen wir jeweils eine bestimmte Zahl aus dem entsprechenden Bereich, setzen diese Zahl in 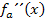ein und überlegen uns das Vorzeichen des Ergebnisses. Beispielsweise kannst du mit 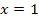aus dem Bereich 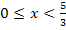arbeiten und mit 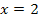aus dem Bereich 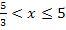. Denke bei der Vorzeichenbestimmung auch daran, dass a für eine negative Zahl steht! Es gilt schließlich: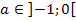

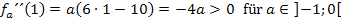
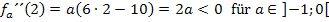
Achtung:Es handelt sich bei 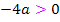und 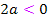nicht etwa um Tippfehler! Beides ist absolut korrekt. – 4a ist wirklich positiv und 2a ist tatsächlich negativ, weil a selbst eine Minuszahl darstellt. Minus mal Minus ergibt schließlich Plus. Die negative Zahl -4 mit der negativen Zahl a multipliziert, ergibt etwas Positives. Deshalb gilt: 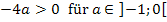Wegen Plus mal Minus ist Minus gilt: 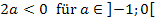, weil die positive Zahl 2 mit der negativen Zahl a multipliziert, etwas Negatives ergibt.

---