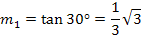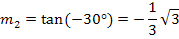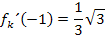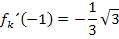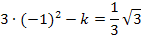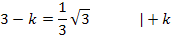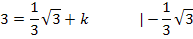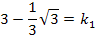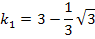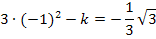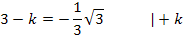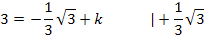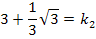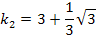Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
| Beginn der Aufgabenstellung | Lösungsweg |
| „Für welchen Wert bzw. für welche Werte von a …?“
Oder: „ Bestimme den Parameter a, so dass …!“ |
Nur den Parameter a berechnen |
| „Welche Funktion bzw. welche Funktionen der Schar …?“ | Vorab den zugehörigen Parameter a berechnen;danach den bzw. die berechneten Werte von a noch (jeweils) in die gegebene Gleichung der Schar  für a einsetzen |
2. Bsp.:
Gegeben ist die Funktionenschar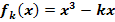 
mit k 
ℝ. Für welche Werte von k schneidet die Tangente an den Graph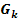 
die x-Achse an der Stelle x = -1 unter einem Winkel von 30°? (2 mögliche Lösungen!)
Lösung:
In der Aufgabe ist nach zwei verschiedenen Lösungen gefragt. Denke daran:Die x-Achse kann an der Stelle x = -1 durch den Graph der Schar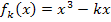 
entweder unter einem Winkel von +30° oder -30° geschnitten werden.
Zuerst ermitteln wir jeweils die Steigung der Tangente, die zu einem Neigungswinkel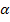 
von +30° bzw. -30° gehört. Dazu verwenden wir die Formel: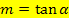 
| 1. Lösung
|
2. Lösung
|
Laut Angabe soll der Graph der Schar 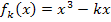die x-Achse an der Stelle x = -1 unter dem Winkel von 30° schneiden. Das bedeutet, dass die Steigung / erste Ableitung von 
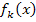an der Stelle x = -1 entweder gleich 
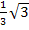oder gleich 
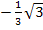sein muss.
| 1. Lösung
|
2. Lösung
|
Wir bilden daher die erste Ableitung: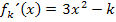 
Nun setzen wir in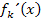 
für x die Zahl -1 ein und setzen das Ergebnis gleich 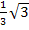bzw. 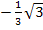. Dadurch ergibt sich:
| 1. Lösung
|
2. Lösung
|
Damit ist die Aufgabe gelöst. Die berechneten Werte von k müssen nicht mehr in die Gleichung der Schar 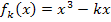eingesetzt werden, denn es war schließlich nur nach den entsprechenden Werten von k gefragt, bei denen die Tangente an den Graph 
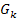die x-Achse bei x = -1 unter einem Winkel von 30° schneidet, und nicht nach den Gleichungen der zugehörigen Funktionen der Schar.
3. Bsp.:
Wir betrachten die Funktionenschar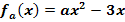 
mit a ℝ und x ℝ. Ihre Graphen werden mit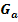 
bezeichnet.
a.) Beschreibe die Graphen 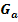der Funktionenschar 
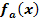mit Worten.
b.) Zeichne die Graphen 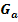für 
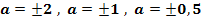und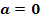 
in ein gemeinsames Koordinatensystem!
c.) Berechne die Nullstellen der Schar in Abhängigkeit von a! Für welchen Wert von a liegt eine der Nullstellen bei x = -1?
d.) Berechne die Koordinaten des Kurvenpunktes von 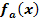in Abhängigkeit von a, in dem die Tangente an 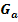waagrecht verläuft! Für welchen Wert von a existiert kein Kurvenpunkt mit waagrechter Tangente?
Lösung:
Zu 3a.
