Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Deshalb muss bei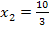 
ein absoluter/globaler Hochpunkt der Schar liegen. Die Randpunkte sind entsprechend absolute/globale Tiefpunkte. Es lässt sich also ohne weitere Rechnung erkennen, dass der Punkt (5|0) ein absoluter/globaler Tiefpunkt der Schar 
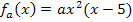mit a 
]-1;0[ und x [0;5] ist. Auch der Punkt (0|0) ist absoluter/globaler Tiefpunkt dieser Schar. (Dabei handelt es sich ebenfalls um ein Randextremum.)
2. Möglichkeit:Art der Extrema mit der zweiten Ableitung ermitteln
Die erste Ableitung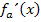 
haben wir schon vorher ermittelt. Wir müssen 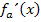also noch einmal ableiten, um 
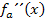zu erhalten. In die zweite Ableitung werden dann nacheinander die beiden berechneten x-Koordinaten 
und 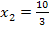eingesetzt. Ergibt sich ein negativer Wert, liegt ein Hochpunkt vor. Erhält man ein positives Ergebnis, handelt es sich um einen Tiefpunkt. Bedenke dabei aber, dass a hier für eine negative Zahl steht! Es gilt schließlich: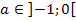 
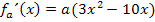
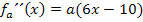
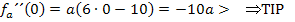
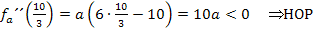
Wir haben somit nachgewiesen:Bei 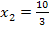liegen die Hochpunkte der Schar 
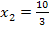. Die x-Koordinate ist unabhängig von a, weil dabei kein a vorkommt. Damit ist gezeigt, dass tatsächlich alle Graphen der Schar ihren Hochpunkt bei haben. Diese x-Koordinate liefert gleichzeitig die waagrechte Entfernung der Dammkrone vom flussabgewandten Rand des Dammes. (Die Dammkrone ist schließlich der höchste Punkt, also der Hochpunkt der Schar.) Die gesuchte Entfernung beträgt 
.
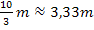Außerdem ist in dieser Teilaufgabe nach der Höhe der Dammkrone in Abhängigkeit von a und für a = -0,15 , a = -0,18 und a = -0,21 gefragt. Die Höhe der Dammkrone ergibt sich aus der y-Koordinate des Hochpunktes. Sie wird zuerst in Abhängigkeit von a berechnet, also ohne etwas Konkretes für a einzusetzen. Wir setzen dazu einfach die bereits ermittelte x-Koordinate des Hochpunktes 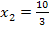in 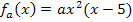ein. In das Ergebnis setzt man anschließend die angegebenen Werte für a ein und erhält so die jeweiligen Dammhöhen für diese konkreten Werte von a.
y-Koordinate der Hochpunkte in Abhängigkeit von a berechnen:
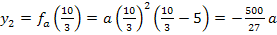
Für a = -0,15 ergibt sich: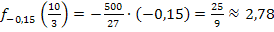 
Höhe der Dammkrone:ca. 2,78 Meter
Für a = -0,18 ergibt sich: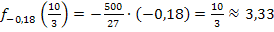 
Höhe der Dammkrone:ca. 3,33 Meter
Für a = -0,21 ergibt sich: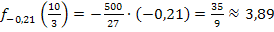 
Höhe der Dammkrone:ca. 3,89 Meter
Hinweis:Die Hochpunkte der Schar haben alle dieselbe x-Koordinate 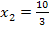;sie unterscheiden sich aber in ihrer y-Koordinate 
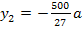. Die x-Koordinate 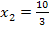ist schließlich unabhängig von a, wogegen die zugehörige y-Koordinate 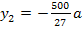noch von a abhängig ist. Für verschiedene Werte von a ergeben sich deshalb unterschiedliche Werte für 
.
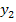