Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Beide x-Koordinaten liegen innerhalb des Intervall x 
[0;5]. 
fällt genau mit dem linken Rand der Definitionsmenge zusammen. Allein aus dem Sachzusammenhang ist natürlich schon klar, dass der gesuchte Hochpunkt nicht bei liegen kann. Also wird wohl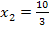 
die x-Koordinate des Hochpunktes sein. Dennoch muss das noch durch Rechnung nachgewiesen werden. Wir müssen also die Art der Extrema bestimmen.
Art der Extrema herausfinden:
1. Möglichkeit:Monotonieuntersuchung
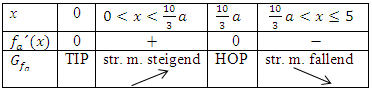
Wir fertigen dazu eine Monotonietabelle für das Intervall x [0;5] an.
| x | 0 |  |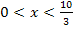
 |
 |
 |
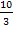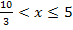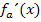0 | 0 | ||
 |
Hier noch einmal die erste Ableitung:
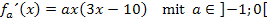
Wir müssen jetzt die Vorzeichen von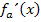 
in den Intervallen 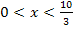und 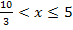ermitteln. Dazu wählen wir jeweils eine konkrete Zahl aus einem der beiden Bereiche, setzen diese Zahl in 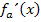ein und überlegen uns das Vorzeichen des Ergebnisses. Beispielsweise kannst du mit 
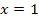aus dem Bereich 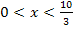arbeiten und mit 
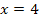aus dem Bereich 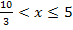. Denke bei der Vorzeichenbestimmung daran, dass a eine negative Zahl darstellt! Es gilt hier schließlich für den Parameter: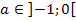 
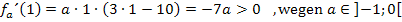
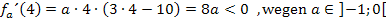
Wir tragen die Vorzeichen und das entsprechende Steigungsverhalten (streng monoton steigend bzw. fallend) in die Monotonietabelle ein. Weil bei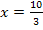 
ein Vorzeichenwechsel der ersten Ableitung vorliegt, handelt es sich dabei wirklich um ein Extremum. Der Vorzeichenwechsel von 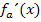ist bekanntlich eine hinreichende Bedingung für einen Extrempunkt. (Würde sich das Vorzeichen der ersten Ableitung nicht ändern, läge nur ein Terrassenpunkt/TEP vor, aber eben kein Extrempunkt.)
Anmerkung:
Streng genommen liegt auch bei x = 5 ein Tiefpunkt vor. (In der Tabelle nicht eingetragen) Es handelt sich dabei um ein sogenanntes Randextremum, d.h. um einen Extrempunkt, der am Rand der Definitionsmenge liegt. Die Schar ist nämlich nur für x [0;5] definiert und nicht für alle reellen Zahlen. Die beiden Ränder der Definitionsmenge x = 0 und x = 5 müssen eigentlich beide gesondert untersucht werden. Es gibt hier jedoch nur eine Stelle innerhalb der Definitionsmenge, wo sich das Vorzeichen der Ableitung und somit die Steigung der Graphen ändert, nämlich 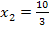. Ändert sich die Monotonie nur an einer einzigen Stelle, liegt an dieser Stelle zwangsläufig ein absolutes/globales Extremum vor. D.h. dort liegt der allerhöchste oder allertiefste Punkt des Graphen. Wegen des Vorzeichenwechsels der Ableitung von + nach – steigen die Graphen der Schar links von 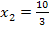und fallen rechts davon.
