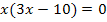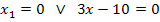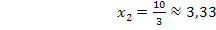Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Hinweis:Der Parameter a muss bei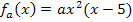 
negativ sein, damit der Graph von 
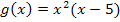an der x-Achse gespiegelt wird. Außerdem soll der Graph von 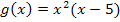entlang der y-Achse gestaucht werden;deshalb muss der Parameter a ein echter Bruch sein. (Ein echter Bruch ist eine Zahl, die vom Betrag her kleiner als 1 ist.) D.h. es muss gelten:a 
]-1;0[
Wenn man für a bei 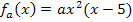verschiedene Werte zwischen -1 und 0 einsetzt, entstehen Funktionen, deren Graphen 
verschiedene mögliche Formen des Dammes darstellen.
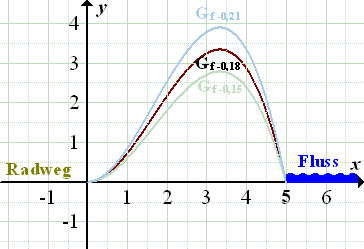
Abb.:Drei ausgewählte Graphen der Schar 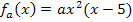. Dargestellt sind die Graphen zu a = -0,15 , a = -0,18 und a = -0,21 im Intervall x [0;5].
Zu 8b.)
Geg.: 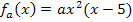mit a ]-1;0[ und x [0;5]
Es soll gezeigt werden, dass die Abszisse x der Hochpunkte aller Graphen der Schar 
unabhängig von a ist und sich somit die waagrechte Entfernung der Dammkrone zum flussabgewandten Rand des Dammes nicht verändert, auch wenn für a verschiedene Werte gewählt werden. Wir müssen also die x-Koordinate (Abszisse) der Hochpunkte der Schar berechnen. Im Ergebnis darf dabei kein a mehr vorkommen, denn nur dann ist die x-Koordinate der Hochpunkte unabhängig von a.
Wir brauchen die erste Ableitung, um die x-Koordinate der Hochpunkte zu berechnen. Wenn du 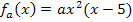in dieser Form direkt ableiten wolltest, müsstest du Die Produktregel verwenden, weil es sich bei 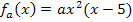um ein Produkt handelt, das in beiden Faktoren die Variable x enthält. Um die Schar besser ableiten zu können, multiplizieren wir vorweg 
in die Klammer hinein. Danach kann die Schar nämlich ganz einfach, also ohne Produktregel, abgeleitet werden. Ob du das a außerhalb der Klammer stehen lässt, oder ob du es zusammen mit dem in die Klammer hineinmultiplizierst, bleibt dir überlassen. Da a hier eine multiplikative Konstante darstellt (d.h. eine Zahl ohne x, mit der multipliziert wird), bleibt der Parameter a beim Ableiten der Schar auf jeden Fall einfach stehen.
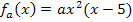
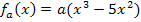
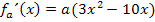
Berechnung der x-Koordinate des Hochpunktes:
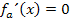
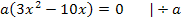
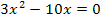
Die vorliegende Gleichung ist gemischtquadratisch, weil sowohl als auch x ohne Potenz vorkommt. Man könnte sie mit der Mitternachtsformel lösen, doch ist das viel zu umständlich. Weil in dieser Gleichung keine Konstante (Zahl ganz ohne x) vorkommt, lässt sich x ausklammern. Dadurch entsteht eine Gleichung der Form „Produkt gleich Null“. Weil ein Produkt gleich Null ist, wenn einer der Faktoren gleich Null ist, darf man die Faktoren einzeln gleich Null setzen.
