Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
c.) Damit der Damm nicht abrutscht, wenn er zum Beispiel durch Regen aufgeweicht wurde, darf er auf der grasüberzogenen, flussabgewandten Seite nicht zu steil angelegt werden. Zeige, dass alle Graphen der Schar unabhängig von a an der gleichen Stelle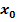 
am stärksten steigen! Wie muss a gewählt werden, damit der Damm auf der flussabgewandten Seite eine Steigung von 1,5 nicht überschreitet?
Lösung:
Zu 8a.)
Mit Hilfe einer Wertetabelle lässt sich der Graph der Funktion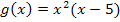 
leicht zeichnen. Es bietet sich an, auf der y-Achse beispielsweise einen Maßstab von 1 cm 
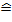5 Meter zu wählen. Für die x-Achse gilt:1 cm 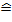1 Meter
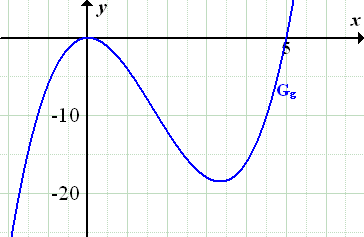
Abb.:Graph 
der Funktion
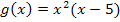
Warum ist die Funktion 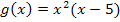nicht geeignet, um die obere Kante des beschriebenen Dammquerschnittes zu beschreiben? Offensichtlich verläuft der Graph der Funktion g im Intervall [0;5] unterhalb der x-Achse. Der Graph müsste aber in diesem Intervall oberhalb der x-Achse verlaufen, damit er für x 
[0;5] der oberen Kante des Dammquerschnittes entsprechen könnte. Man muss den Graph 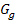also auf jeden Fall an der x-Achse spiegeln. Wenn Herr Müller ein Minuszeichen vor den Funktionsterm von g schreiben würde, würde der Graph 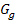an der x-Achse gespiegelt. Es ergäbe sich dann die Funktion 
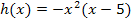. Leider passt auch diese Funktion noch nicht ganz. Ihr Graph muss nämlich noch entlang der y-Achse gestaucht werden, weil sonst der Damm viel zu hoch werden würde. Das kannst du leicht rechnerisch kontrollieren, indem du beispielsweise x = 3 in die Funktion 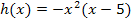einsetzt.
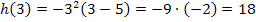
In 3 Meter Abstand von der linken Seite aus hätte der Damm somit eine Höhe von 18 Metern. Der Damm wäre also definitiv viel zu hoch, wenn die obere Kante seines Querschnittes durch die Funktion 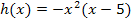beschrieben würde.
Leider wissen wir nicht, wie stark die Funktion 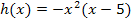entlang der y-Achse gestaucht werden soll, weil die Höhe des Dammes nicht genau vorgegeben ist. Deshalb kann man Herrn Müller bloßden Rat geben, einen Parameter einzuführen. Wir bezeichnen diesen Parameter hier mit a. Wenn a für irgendeine positive Zahl steht, die kleiner ist als 1, muss Herr Müller die Funktion 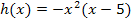einfach mit a multiplizieren und schon ergibt sich eine mehr oder weniger in y-Richtung gestauchte Funktion. Er könnte also die Schar 
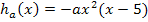mit a ]0;1[ und x [0;5] nehmen. Er kann aber das Minuszeichen bei der Schar 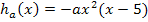auch einfach weglassen, wenn er stattdessen den Parameter a als negative Zahl auffasst. Das wäre am praktischsten. Er sollte also mit der Schar 
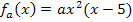mit a ]-1;0[ und x [0;5] arbeiten.
