Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Den oberen Rand des Dammquerschnitts versucht Herr Müller durch eine ganzrationale Funktion 3. Grades zu modellieren. Den Ursprung des Koordinatensystems legt er dabei so, dass er mit dem Punkt zusammenfällt, wo der Damm waagrecht ausläuft. Vergleiche Skizze! Auf beiden Achsen gilt in dieser Skizze 1 cm in der Zeichnung entspricht 1 Meter in Realität, also ein Maßstab von 1 :100.
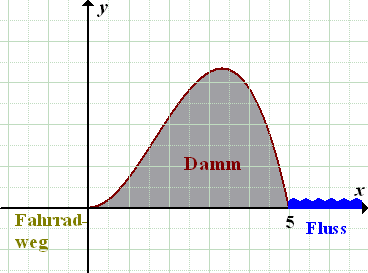
Abb.:Querschnitt durch den geplanten Damm mit links angrenzendem Fahrradweg und rechts angrenzendem Fluss (Skizze von Herrn Müller)
Die gesuchte Funktion soll f (x) heißen. Herr Müller versucht nun die Gleichung der Funktion f (x) zu ermitteln. Du sollst ihn dabei unterstützen.
Wie du sicher weißt, berührt der Graph einer Funktion die x-Achse, wenn sie dort eine doppelte Nullstelle hat. Bei x = 0 berührt die gesuchte Funktion die x-Achse offensichtlich, deshalb muss dort eine doppelte Nullstelle der Funktion liegen. (Siehe auch:Vielfachheiten der Nullstellen) Bei einer einfachen Nullstelle wird die x-Achse dagegen geschnitten. Dies ist hier bei x = 5 der Fall;deshalb muss die gesuchte Funktion dort eine einfache Nullstelle haben. Kennt man alle Nullstellen, lässt sich die Gleichung einer Funktion in ihrer faktorisierten Form besser aufstellen, als in der ausmultiplizierten Form. (Näheres dazu auch bei:Faktorisierter Funktionsterm)
Herr Müller hat die Idee, zuerst die Gleichung einer möglichst einfachen Funktion aufzustellen, die bei x = 0 eine doppelte Nullstelle und bei x = 5 eine einfache Nullstelle besitzt, die aber wahrscheinlich noch nicht ganz dem Dammquerschnitt entspricht. So kommt er zu der Funktion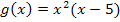 
.
a.) Skizziere den Graph der Funktion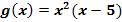 
im Intervall [-2;5,5]! Was muss man an der Funktionsgleichung von g ändern, damit sie als Funktion f (x) für den oben beschrieben Sachzusammenhang verwendbar ist? Führe dazu einen geeigneten Scharparameter ein und gib die Gleichung einer Schar an, welche die verschiedenen möglichen Verläufe der Oberkante des Dammquerschnitts beschreibt!
b.) Die Graphen der Schar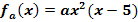 
mit a 
]-1;0[ und x [0;5] stellen die Oberkante verschiedener möglicher Dammquerschnitte dar. Zeige, dass die Abszisse x der Hochpunkte aller Graphen der Schar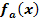 
unabhängig von a ist und sich somit die waagrechte Entfernung der Dammkrone zum flussabgewandten Rand des Dammes nicht verändert, auch wenn für a verschiedene Werte gewählt werden! Wie lang ist diese waagrechte Entfernung der Dammkrone zum flussabgewandten Rand des Dammes? Berechne außerdem die Höhe der Dammkrone in Abhängigkeit von a und für a = -0,15 , a = -0,18 und a = -0,21!
