Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Nur die Koordinaten des Punkts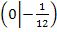 
sind schließlich völlig unabhängig von a. Der zweite Wendepunkt 
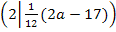hat zwar eine von a unabhängige x-Koordinate, aber seine y-Koordinate ist von a abhängig. Deshalb gibt es zwar zwei verschiedene Wendepunkte, die beide eine von a unabhängige x-Koordinate besitzen, aber nur einen Wendepunkt, der auch eine von a unabhängige y-Koordinate besitzt. Dies ist der gesuchte Punkt 
.
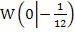2. Möglichkeit
Wir setzen x = 0 in die dritte Ableitung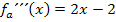 
ein und zeigen, dass das Ergebnis ungleich Null ist.
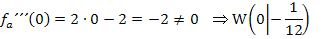
Damit haben wir gezeigt, dass es genau einen gemeinsamen Wendepunkt aller Graphen der Schar gibt. Er hat die Koordinaten 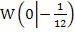. Fertig!
Anmerkung:Interessant ist an dieser Schar auch, dass der zweite Wendepunkt ebenfalls eine von a unabhängige x-Koordinate hat. Bei dem zweiten Wendepunkt 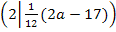ergeben sich aber jeweils unterschiedliche y-Koordinaten, wenn man verschiedene Werte für a einsetzt. Diese Wendepunkte liegen alle auf der Gerade x = 2 senkrecht übereinander. Die Ortslinie dieser Wendepunkte hat somit die Gleichung x = 2.
Damit du dir das Ganze besser vorstellen kannst, hier noch eine Abbildung, in der einige ausgewählte Graphen der Schar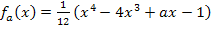 
gemeinsam mit der Ortslinie der zweiten Wendepunkte dargestellt sind.
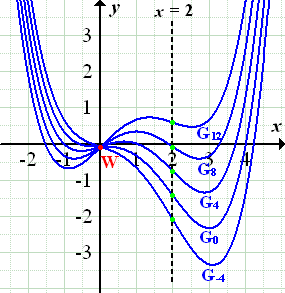
Abb.:Die Graphen der Schar 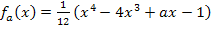mit a = -4;0;4;8;12 zusammen mit der Ortslinie x = 2 der zweiten Wendepunkte. Der gemeinsame Wendepunkt 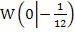aller Graphen der Schar ist rot markiert. Jeder Graph dieser Schar besitzt neben dem Wendepunkt W noch einen zweiten Wendepunkt;dieser ist jeweils grün markiert. Diese Wendepunkte liegen alle auf der schwarz gestrichelten Geraden. Deshalb ist diese Gerade die Ortslinie der zweiten Wendepunkte.
Bisher haben wir uns ausschließlich mit Aufgaben befasst, bei denen die Gleichung der Schar bereits angegeben war. Vielleicht möchtest du aber auch noch wissen, wie man überhaupt auf die Gleichung einer Schar kommt und welche Probleme im Alltag oder Beruf sich mit Hilfe von Scharen lösen lassen. Daher als nächstes eine Beispielaufgabe, an Hand derer gezeigt wird, wie man mit Hilfe von Scharen Funktionen modellieren kann. Damit ist gemeint, dass die Gleichung einer bestimmten Kurve gesucht ist, von der bestimmte Eigenschaften bekannt sind.
8. Bsp.:Planung eines Dammes
Der Architekt Herr Müller hat den Auftrag erhalten einen Damm für den lokalen Fluss zu planen. Der Damm soll mit Erde aufgeschüttet und auf der flacheren, flussabgewandten Seite komplett mit Rasen überzogen werden. Der untere Teil der steileren, flusszugewandten Seite wird mit einer Betonschicht beschichtet. So soll der Damm einen Schutz gegen Überflutungen bei Hochwasser des Flusses bieten. Vorgesehen ist für den Damm eine Gesamtbreite von 5 Metern. Die Dammkrone soll eine Höhe von mindestens 2,5 Metern haben, aber auch nicht höher als 5,5 Meter sein. Auf der flussabgewandten Seite soll der Damm waagrecht auslaufen, da direkt daneben parallel zu dem Damm ein Spazier- und Radweg verlaufen soll.
