Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

Vorweg bilden wir die ersten drei Ableitungen.

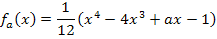
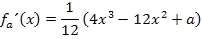
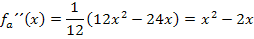
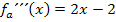
Berechnung der x-Koordinaten der Wendepunkte:

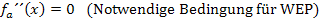
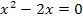
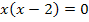
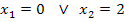
Beide x-Koordinaten sind unabhängig von a, weil es sich um normale Zahlen ohne a handelt. Eine von den beiden muss die x-Koordinate des gesuchten Punktes W sein. Welche das ist, lässt sich momentan noch nicht sagen. Erstens wissen wir noch gar nicht, ob an diesen beiden Stellen überhaupt jeweils ein Wendepunkt vorliegt und außerdem haben wir die zugehörigen y-Koordinaten noch nicht berechnet. (Auch die y-Koordinate des Punktes W muss unabhängig von a sein, damit W gemeinsamer Wendepunkt aller Graphen der Schar sein kann.) Deshalb ermitteln wir jetzt die zugehörigen y-Koordinaten.

Berechnung der y-Koordinaten:

Wir setzen die berechneten x-Koordinaten jeweils in 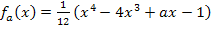ein.

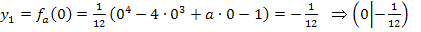
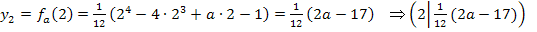
Die zweite y-Koordinate ist abhängig von a, weil bei 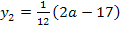noch ein a vorkommt. Der Punkt 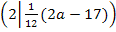kann also nicht der gesuchte Punkt W sein, weil er nicht gemeinsamer Punkt aller Graphen der Schar ist. Vermutlich lauten die Koordinaten des Punktes W daher 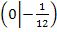. Es muss aber noch gezeigt werden, dass es sich dabei wirklich um einen Wendepunkt handelt.

Nachweis des Wendepunktes:

1. Möglichkeit

Wir weisen den Vorzeichenwechsel der zweiten Ableitung z. B. mit einer Krümmungstabelle nach.

Krümmungstabelle an.

x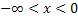
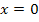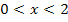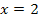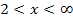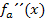		0		0

Hier noch einmal die zweite Ableitung:

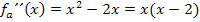
Wir müssen jetzt die Vorzeichen von 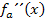in den Intervallen 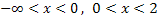und 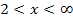ermitteln. Dazu wählen wir jeweils eine bestimmte Zahl aus dem entsprechenden Bereich, setzen diese Zahl in 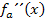und überlegen uns das Vorzeichen des Ergebnisses. Beispielsweise kannst du mit 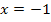aus dem Bereich 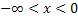arbeiten, mit 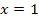aus dem Bereich 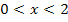und mit 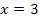aus dem Bereich .

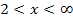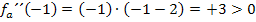
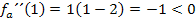
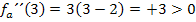
Wir tragen die Vorzeichen und das entsprechende Krümmungsverhalten (links- bzw. rechtsgekrümmt) in die Krümmungstabelle ein. Weil bei x = 0 und x = 2 jeweils ein Vorzeichenwechsel der zweiten Ableitung vorliegt, handelt es sich bei beiden Stellen wirklich um Wendestellen. Der Vorzeichenwechsel von 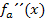ist bekanntlich eine hinreichende Bedingung für einen Wendepunkt. Würde sich das Vorzeichen der zweiten Ableitung nicht ändern, läge nur ein Flachpunkt/FLAP vor, aber eben kein Wendepunkt. Mehr dazu bei:Zweite Ableitung f´´(x)

x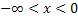
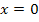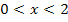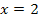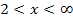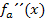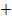		0		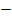0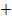
	linksgekr.	WEP	rechtsgekr.	WEP	linksgekr.

Wir interessieren uns natürlich hauptsächlich für die Stelle x = 0.

---