Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
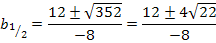
Das Ergebnis sieht so extrem hässlich aus;wir müssen es noch irgendwie vereinfachen. (Ein wirklich „schönes“ Ergebnis kommt hier leider sowieso nicht heraus, aber ein bisschen Kosmetik lässt sich noch betreiben.) Da im Zähler eine Summe bzw. Differenz vorliegt, darf nicht gekürzt werden. Was man allerdings machen kann, ist folgendes:Jeden Summanden des Zählers einzeln durch den Nenner -8 teilen.
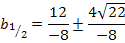
Jetzt kann man nämlich bei beiden Brüchen mit 4 kürzen.
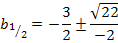
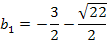
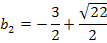
Damit ist diese Aufgabe gelöst. Für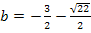 
oder 
berührt die Scharparabel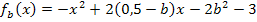 
die Gerade 
.
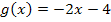Du wunderst dich darüber, dass es zwei Lösungen für b gibt, obwohl es nur einen gemeinsamen Punkt von Gerade und Parabel geben soll?
Erklärung:Wenn man einen der beiden Werte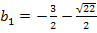 
oder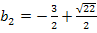 
für b bei der Schar 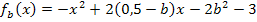einsetzt, ergibt sich jeweils eine Parabel, die mit der Gerade 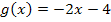genau einen Punkt gemeinsam hat. Es existieren also zwei Parabeln der Schar, welche die Gerade als Tangente haben und somit jeweils genau einen gemeinsamen Punkt mit der Gerade besitzen. In der folgenden Abbildung sind diese beiden Scharparabeln in grün dargestellt.
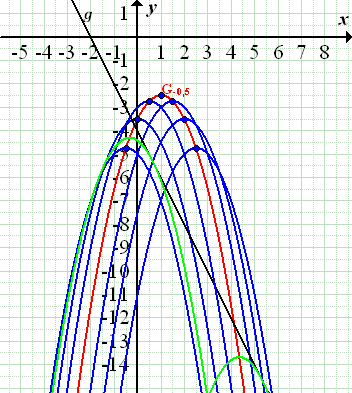
Abb.:Einige Graphen der Schar 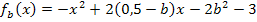zusammen mit der Geraden 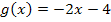. In grün sind die beiden Scharparabeln für 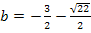und dargestellt;nur diese zwei Scharparabeln werden von der Gerade in genau einem Punkt berührt.
7. Bsp.:
Wir betrachten die Schar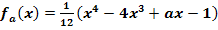 
mit a 
ℝ. Zeige, dass es genau einen Punkt W gibt, der gemeinsamer Wendepunkt aller Graphen dieser Schar ist! Gib auch die Koordinaten von W an!
Lösung:
Damit ein Punkt gemeinsamer Wendepunkt aller Graphen der Schar sein kann, müssen seine Koordinaten beide unabhängig vom Scharparameter a sein. Weder bei der x- noch bei der y-Koordinate dieses Wendepunktes darf also der Parameter a vorkommen. Wir berechnen daher zuerst alle Wendepunkte der Schar und schauen dann, welcher dieser Punkte völlig unabhängig ist von a. Weil wir zeigen sollen, dass es genau einen gemeinsamen Wendepunkt aller Graphen der Schar 
gibt, wird sich zwangsläufig nur ein derartiger Punkt ergeben. Dies ist der gesuchte Punkt W.
Zur Erinnerung:Die x-Koordinaten der Wendepunkte berechnet man, indem man die zweite Ableitung gleich Null setzt und nach x auflöst. Danach weist man nach, dass sich das Vorzeichen der zweiten Ableitung an dieser Stelle ändert (z.B. mit einer Krümmungstabelle) oder man setzt die berechneten x-Koordinaten in die dritte Ableitung ein und zeigt, dass dabei nicht Null herauskommt.
