Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Es muss deshalb gelten:D = 0
Deshalb berechnen wir nun bloßdie Diskriminante D und verwenden nicht die gesamte Mitternachtsformel. Die Diskriminante setzen wir anschließend gleich Null. So erhalten wir eine Gleichung, mit der wir b berechnen können.
Hier noch einmal die Gleichung von oben:
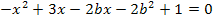
Versuche nun die Diskriminante selbständig zu berechnen! Dabei tritt eine Schwierigkeit auf. Welche das ist, wirst du bestimmt selbst merken.
Wahrscheinlich stehst du jetzt vor dem Problem, dass du nicht weißt, was in dieser Gleichung den Koeffizienten a, b und c aus der Mitternachtsformel entspricht. Das a dürfte noch klar sein:a = -1 (a ist schließlich die Zahl, die in unserer Gleichung vor 
steht.) Problematisch wird es aber bei dem b aus der Mitternachtsformel. Das b aus der Mitternachtsformel entspricht an sich der Zahl bzw. dem Ausdruck, der in der Gleichung vor x steht. Doch leider kommen in unserer Gleichung zwei Terme mit x vor, nämlich 3x und -2bx. Wegen des Parameters b lassen sich 3x und -2bx nicht so leicht zusammenfassen. Da hilft bloßein kleiner Trick:Aus 3x und -2bx das x ausklammern! Wir schreiben das ausgeklammerte x dabei ausnahmsweise nach hinten, also hinter die entstehende Klammer.
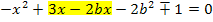
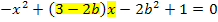
In dieser Form kannst du bestimmt leicht erkennen, was in dieser Gleichung jeweils dem a, b und c aus der Mitternachtsformel entspricht. (Dem b aus der Mitternachtsformel entspricht der gesamte Ausdruck vor dem x. Vergleiche blau geschriebenen Ausdruck unten! Dem c aus der Mitternachtsformel entspricht der gesamte Ausdruck am Ende;also das, was ganz ohne x in der Gleichung vorkommt. Vergleiche lila geschriebenen Ausdruck in der nächsten Zeile!)
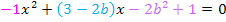
Die Diskriminante D ist jetzt leicht zu berechnen:
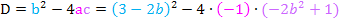
Wir vereinfachen die Diskriminante D noch etwas, bevor wir sie gleich Null setzen. Um die erste Klammer zu quadrieren verwenden wir die zweite binomische Formel: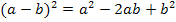 
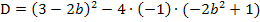
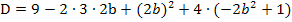
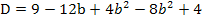
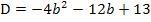
Nun setzen wir die Diskriminante gleich Null, da wir b so berechnen sollen, dass die Gerade mit der Scharparabel genau einen gemeinsamen Punkt hat.
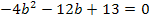
Die nun vorliegende Gleichung ist gemischtquadratisch, weil neben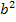 
auch b ohne Potenz vorkommt. Jetzt ist allerdings b die Unbekannte, nach der aufgelöst werden muss. Wir verwenden die komplette Mitternachtsformel, um die Gleichung nach b aufzulösen. (Jetzt reicht es nicht, nur die Diskriminante zu verwenden! Wir wollen schließlich nicht nur wissen, wie viele Lösungen es für b gibt, sondern wir wollen die entsprechenden Werte von b wirklich ausrechnen.
