Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
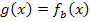
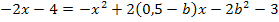
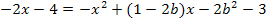
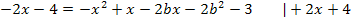
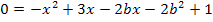
Die vorliegende Gleichung ist eine Gleichung 2. Grades, also eine quadratische Gleichung, weil 
die höchste auftretende Potenz der Unbekannten x ist. Es kann also höchstens zwei verschiedene Lösungen für x geben. Genauer gesagt ist die Gleichung gemischtquadratisch;sie enthält schließlich neben auch x ohne Potenz. Wir müssen diese Gleichung gar nicht nach x auflösen. Wir wollen schließlich bloßherausfinden, für welche Werte von b sich genau eine Lösung für x ergibt. Weil die vorliegende Gleichung gemischtquadratisch ist und dabei auch eine Konstante (Zahl oder Ausdruck ohne x) vorkommt, lässt sich x nicht ausklammern oder die Wurzel ziehen. Die Gleichung würde sich jedoch mit der Mitternachtsformel lösen lassen.
Zur Erinnerung:
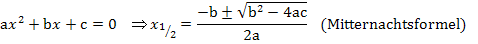
Der Ausdruck unter der Wurzel in der Mitternachtsformel ist die Diskriminante:
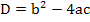
Die Anzahl der reellen Lösungen einer gemischtquadratischen Gleichung hängt nur von der Diskriminante ab.
D >0: 
2 Lösungen
D <0: 0 Lösungen
D = 0: 1 Lösung
Hinweis:Zur Unterscheidung des Scharparameters b von dem Koeffizienten b aus der Mitternachtsformel wurde auf dieser website für den Scharparameter die Kursivschreibweise b gewählt und für den Koeffizienten b aus der Mitternachtsformel die nicht kursive Schreibweise b. Das kursiv geschriebene b steht in dieser Aufgabe also immer für den Scharparameter der Schar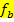 
, wogegen das normal geschriebene b für den Koeffizienten aus der Mitternachtsformel steht. Unterscheide also genau zwischen Scharparameter b und dem b aus der Mitternachtsformel!
Zwei Lösungen ergeben sich aus der Mitternachtsformel, wenn die Diskriminante D (d.h. der Ausdruck unter der Wurzel in der Mitternachtsformel) positiv ist. Erklärung:Aus einer positiven Zahl D lässt sich die Wurzel zumindest näherungsweise ziehen. Wegen des Plus/Minus-Zeichens vor der Wurzel in der Mitternachtsformel erhält man dann zwei verschiedene Lösungen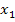 
und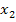 
.
Keine Lösung ergibt sich, wenn die Diskriminante D negativ ist, weil sich aus einer negativen Zahl die Wurzel nicht ziehen lässt.
Genau eine Lösung ergibt sich aus der Mitternachtsformel, wenn die Diskriminante D gleich Null ist.
Wir suchen hier diejenigen Werte von b, für die sich genau eine Lösung ergibt.
