Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Wegen der Konstanten 12 auf der rechten Seite der Gleichung bringt uns das Ausklammern von a hier nichts. Durch das Ausklammern von a auf der rechten Seite der Gleichung würde sich nur eine Gleichung der Form „Produkt gleich 12“ ergeben, was uns aber nichts brächte. Nur bei Gleichungen der Form „Produkt gleich Null“ kann man die Faktoren einzeln gleich Null setzen, weil ein Produkt gleich Null ist, wenn einer der Faktoren gleich Null ist. Bei Gleichungen der Form „Produkt gleich Zahl ungleich Null“ geht das natürlich nicht. Da neben 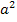 und a auch noch die Konstante 12 in der Gleichung vorkommt, bringt das Ausklammern von a hier also nichts. So eine Gleichung lässt sich aber mit der Mitternachtsformel lösen. Allerdings muss dafür die Gleichung vorher so umgestellt werden, dass auf einer Seite die Zahl Null steht. Wir bringen daher die 12 auf die linke Seite der Gleichung. Dann könntest du gleich in die Mitternachtsformel einsetzen. In diesem Fall bietet es sich jedoch an, vorweg noch alles durch 6 zu teilen. Dadurch werden die Zahlen kleiner und es lässt sich dann leichter rechnen.
und a auch noch die Konstante 12 in der Gleichung vorkommt, bringt das Ausklammern von a hier also nichts. So eine Gleichung lässt sich aber mit der Mitternachtsformel lösen. Allerdings muss dafür die Gleichung vorher so umgestellt werden, dass auf einer Seite die Zahl Null steht. Wir bringen daher die 12 auf die linke Seite der Gleichung. Dann könntest du gleich in die Mitternachtsformel einsetzen. In diesem Fall bietet es sich jedoch an, vorweg noch alles durch 6 zu teilen. Dadurch werden die Zahlen kleiner und es lässt sich dann leichter rechnen.
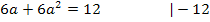
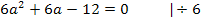
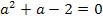
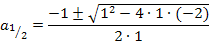
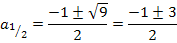
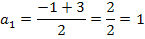
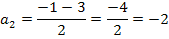
Dies ist schon die Lösung. Für 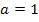 und
und 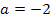 verläuft die Tangente des Graphen
verläuft die Tangente des Graphen 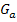 an der Stelle x = 2 parallel zur Geraden
an der Stelle x = 2 parallel zur Geraden 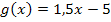 . Die zugehörigen Gleichungen der Funktionen
. Die zugehörigen Gleichungen der Funktionen 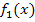 zu
zu 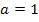 und
und 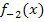 zu
zu 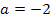 waren gar nicht gefragt. Es war wirklich nur nach den jeweiligen Werten von a gefragt! Deshalb muss man hier die berechneten Werte
waren gar nicht gefragt. Es war wirklich nur nach den jeweiligen Werten von a gefragt! Deshalb muss man hier die berechneten Werte 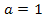 und
und 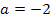 nicht mehr in
nicht mehr in 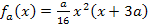 einsetzen. Das hätte man nur dann machen müssen, wenn explizit gefragt gewesen wäre, für welche Funktionen der Schar die Tangente des Graphen
einsetzen. Das hätte man nur dann machen müssen, wenn explizit gefragt gewesen wäre, für welche Funktionen der Schar die Tangente des Graphen 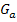 an der Stelle x = 2 parallel zur Geraden
an der Stelle x = 2 parallel zur Geraden 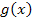 verläuft.
verläuft.
Es ist also ein Unterschied, ob nur nach den Werten von a gefragt ist, für die eine bestimmte Bedingung erfüllt ist, oder ob danach gefragt ist, welche Funktionen der Schar eine bestimmte Bedingung erfüllen.
Ist bloßnach den Werten des Parameters a gefragt, für die eine bestimmte Bedingung erfüllt ist, aber nicht nach den zugehörigen Funktionen der Schar, reicht es vollkommen aus, wenn man a entsprechend berechnet. Das Einsetzen der berechneten Werte von a in die Gleichung der Schar  ist dann nicht mehr nötig.
ist dann nicht mehr nötig.
Sind jedoch bestimmte Funktionen der Schar gefragt, für die eine bestimmte Bedingung erfüllt ist, und nicht nur die zugehörigen Werte von a, musst du den Parameter zuerst entsprechend berechnen und danach zusätzlich noch in die Gleichung der Schar  einsetzen. Erst durch das Einsetzen der jeweiligen Werte von a in die Gleichung von
einsetzen. Erst durch das Einsetzen der jeweiligen Werte von a in die Gleichung von  erhältst du die gesuchte(n) Funktion(en) der Schar.
erhältst du die gesuchte(n) Funktion(en) der Schar.
Achte also genau auf die Fragestellung!

