Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Wir berechnen dazu einfach die y-Koordinate des Punktes P, der auf der Geraden g liegt und der dieselbe x-Koordinate hat wie der Scheitel S(1|-2,5). D.h. wir ermitteln die y-Koordinate des Geradenpunktes P(1|?), damit wir sie anschließend mit der y-Koordinate des Scheitels S(1|-2,5) vergleichen können. Die y-Koordinate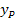 
des Geradenpunktes 
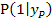erhält man, indem man die x-Koordinate von P, also x = 1 in die Geradengleichung 
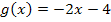einsetzt.
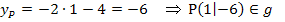
Die y-Koordinate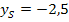 
des Scheitels S(1|-2,5) ist größer als die y-Koordinate 
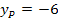des Punktes P(1|-6):
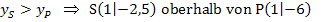
Weil die Parabel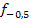 
nach unten geöffnet ist und ihr Scheitel oberhalb der Geraden g liegt, ist es logisch, dass die Parabel 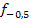mit der Geraden 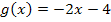genau zwei gemeinsame Punkte haben muss.
Alle anderen Parabeln der Schar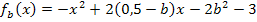 
liegen tiefer als die Parabel 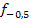. Wie viele gemeinsame Punkte die anderen Parabeln der Schar 
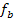mit der Geraden g haben, kann man nicht direkt sagen;das hängt vom Parameter b ab. Zwei Parabeln der Schar berühren die Gerade nur in einem Punkt. (Welche das sind, werden wir in Teilaufgabe 6c. ermitteln.) Einige der Scharparabeln liegen sogar unterhalb der Geraden, so dass sie gar keinen gemeinsamen Punkt mit der Gerade besitzen.
In der Aufgabe ist aber nur gefragt, wie viele gemeinsame Punkte die Gerade g mit einer Parabel der Schar 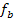höchstens haben kann. Da die Parabel 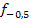der Schar 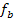mit der Geraden g nachgewiesenermaßen zwei gemeinsame Punkte hat, gibt es auf jeden Fall schon mal mindestens eine Parabel der Schar, die zwei Punkte mit der Geraden g gemeinsam hat. Mehr als zwei gemeinsame Punkte kann eine Parabel mit einer Geraden niemals haben. Also hat eine Parabel der Schar 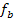höchstens zwei gemeinsame Punkte mit der Geraden g.
Damit ist diese Teilaufgabe gelöst.
Zu 6c.)
Es ist die Frage zu beantworten, für welche Werte von b die Funktionen der Schar 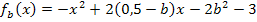jeweils die Gerade 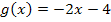berühren.
Hinweis:Bitte im Folgenden nicht runden, sondern die exakten Werte von b berechnen! Diese Teilaufgabe hat etwas sonderbare Ergebnisse;bitte trotzdem nicht denken, dass die Ergebnisse falsch sind.
Weil die Gerade g eine der Scharparabeln berühren soll, muss die Gerade eine Tangente an die jeweilige Scharparabel sein. Eine Tangente hat bekanntlich genau einen gemeinsamen Punkt mit einer Parabel. Wir müssen daher herausfinden, für welche Werte von b genau ein gemeinsamer Punkt von Parabel und Gerade existiert.
Einige hilfreiche Informationen zum Thema „Anzahl gemeinsamer Punkte zweier Funktionen“
Um b so zu bestimmen, dass die Gerade 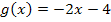mit einer der Scharparabeln 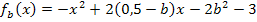genau einen gemeinsamen Punkt hat, müssen wir die Gerade g erst einmal mit der Schar 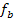gleichsetzen und dann schauen, für welches b genau eine Lösung für x herauskommt.
