Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Zu 6b.)
Es ist die Frage zu beantworten, wie viele gemeinsame Punkte die Gerade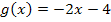 
mit einer Funktion der Schar 
höchstens haben kann? In der Aufgabenstellung ist bloßeine kurze Begründung verlangt. Das weist schon darauf hin, dass keine ausführliche Rechnung verlangt ist, sondern nur eine Überlegung.
Zur Erinnerung:
Eine Gerade kann mit einer Parabel keinen, genau einen oder zwei gemeinsame Punkte besitzen.
Allgemein gilt also, dass eine Parabel mit einer Gerade höchstens zwei gemeinsame Punkte besitzen kann.
Doch wie ist das in unserem speziellen Fall? Die Gerade hat die Gleichung 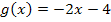und die Parabel soll zu der Schar 
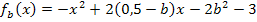gehören.
Die Gerade g kannst du dir hoffentlich vorstellen:Sie schneidet die y-Achse bei -4 und hat außerdem die Steigung -2, d.h. man geht beim Steigungsdreieck 1 nach rechts und 2 nach unten. (In der Abbildung etwas weiter unten kannst du die Gerade g zusammen mit einigen Graphen der Schar sehen.)
Die Scharparabeln sind alle nach unten geöffnet;ihre Scheitel liegen auf der Ortskurve der HOP / Scheitel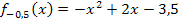 
. Das besondere an der Schar 
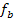ist, dass die Ortskurve der Scheitelpunkte selbst zur Schar 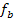gehört. Vergleiche Teilaufgabe 6a.!
Für b = -0,5 ergibt sich die Ortskurve der Scheitel. Die Kurve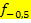 
ist die am höchsten liegende Parabel der Schar 
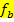. Der Scheitel von 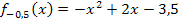lässt sich schnell berechnen, weil wir in Teilaufgabe 6a. bereits ermittelt haben, dass die Hochpunkte/Scheitel der Schar 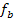die Koordinaten 
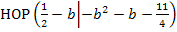haben. Um den Scheitel von 
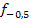zu bekommen, muss man nur für b den Wert -0,5 bzw. 
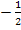einsetzen:
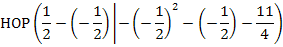
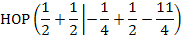
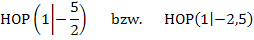
Der Hochpunkt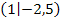 
ist somit der Scheitel S(1|-2,5) von 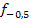. Der Scheitel S(1|-2,5) liegt oberhalb der Geraden 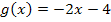. Betrachte dazu die nachfolgende Abbildung! Da die Parabel 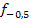nach unten geöffnet ist und ihr Scheitel oberhalb der Geraden g liegt, schneidet die Parabel 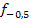die Gerade g zwangsläufig genau zweimal.
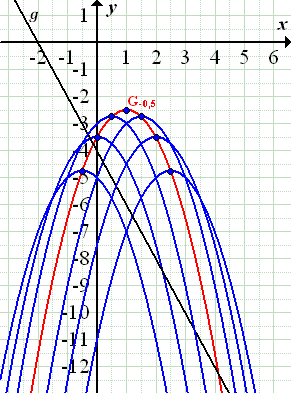
Abb.:Einige Graphen der Schar 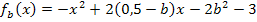zusammen mit der Geraden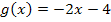
Die Ortskurve der Scheitel ist rot dargestellt;es handelt sich dabei um die Scharparabel 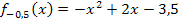. Sie hat offensichtlich zwei gemeinsame Punkte mit der Geraden g. Alle anderen Parabeln der Schar liegen unterhalb von 
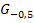, sie haben entweder zwei, einen oder auch keinen gemeinsamen Punkt mit der Gerade g. Damit ist eigentlich bereits klar, dass die Gerade g höchstens zwei gemeinsame Punkte mit einer der Scharparabeln besitzt.
Dass der Scheitel S(1|-2,5) der Parabel 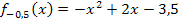tatsächlich oberhalb der Geraden 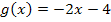liegt, kann auch rechnerisch nachgewiesen werden.
