Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Alle Parabeln der Schar haben deswegen die gleiche Form;sie sind nur mehr oder weniger nach oben / unten bzw. zur Seite verschoben.) Eine nach unten geöffnete Parabel hat nur ein einziges Extremum, nämlich ihren Scheitel, und der ist bei einer nach unten geöffneten Parabel zwangsläufig ein Hochpunkt. Daher sparen wir uns hier den Nachweis, dass es sich für b 
ℝ bei dem vorliegenden Extremum um einen Hochpunkt handelt.)
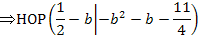
Berechnung der Ortskurve:
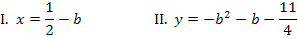
Wir lösen Gleichung I. nach b auf und setzen das Ergebnis bei II. für jedes darin vorkommende b ein.
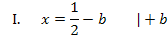
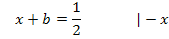
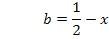
b in II.:
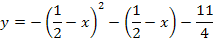
Die vordere Klammer wird mit Hilfe der zweiten binomischen Formel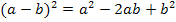 
ausgerechnet.
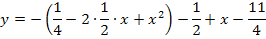
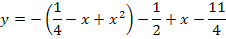
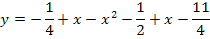
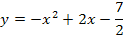
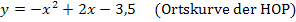
Berechnung der Ortskurve der HOP (2. Methode)
Wie man die x-Koordinate des Hochpunktes berechnet, haben wir bei der ersten Methode schon besprochen. Wir wollen das nicht noch einmal durchrechnen. Wir gehen daher von der x-Koordinate des Hochpunktes der Schar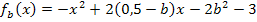 
aus:
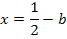
Um die Ortskurve der Hop zu erhalten, ohne die y-Koordinate des HOP zu berechnen, lösen wir die Gleichung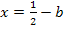 
nach b auf und setzen das Ergebnis für b in die Gleichung der Schar 
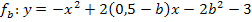ein. Dann vereinfachen wir die entstehende Gleichung und schon haben wir die gesuchte Ortskurve ermittelt.
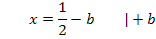
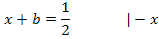
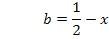
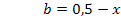
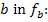
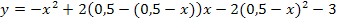
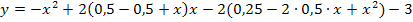
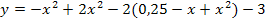
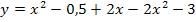
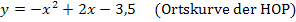
Die x-Koordinate der HOP 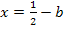kann wegen b ℝ alle reellen Zahlen annehmen. Die Ortskurve ist daher für x ℝdefiniert.
Nun kennen wir die Gleichung der gesuchten Ortskurve der Hochpunkte. Es bleibt die Frage zu klären, ob die Ortskurve selbst zu der Schar 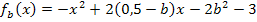gehört. Die Schar 
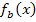besteht ausschließlich aus nach unten geöffneten Normalparabeln. Auch die Ortskurve der HOP ist eine nach unten geöffnete Normalparabel, weil bei der Ortskurve 
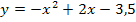der Öffnungsfaktor (d.h. die Zahl vor dem 
) ebenfalls -1 ist. Die Ortskurve könnte also eventuell tatsächlich zu der Schar 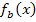gehören. Um dies genau sagen zu können, vergleichen wir die Koeffizienten der Schar mit denen der Ortskurve.
Schar: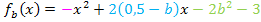 
Ortskurve: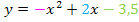 
Es ist also die Frage zu klären, für welchen Wert von b der Koeffizient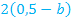 
gleich 
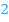wird und ob sich für diesen Wert von b bei 
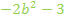genau der Wert 
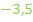ergibt.
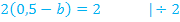
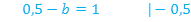
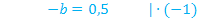
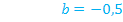
Nun müssen wir überprüfen, ob sich für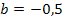 
bei 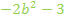genau der Wert 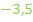ergibt.
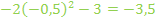
Auch das stimmt. Für 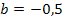ergibt sich aus 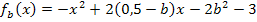genau die Gleichung der Ortskurve der HOP.
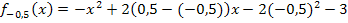
Die Ortskurve der HOP gehört also in diesem Beispiel tatsächlich zu der Schar 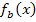. Das ist natürlich nicht die Regel. Bei den meisten anderen Aufgaben zum Thema „Ortskurven“ wird das eher nicht der Fall sein. Es handelt sich bei diesem Beispiel also um einen interessanten Sonderfall.
