Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Die erste Ableitung haben wir oben bereits gebildet;sie lautet:
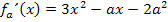
Weil es um die Steigung der Tangente an der Stelle x = 0 geht, müssen wir für x die Zahl 0 in die Ableitung einsetzen. Das Ergebnis setzen wir gleich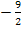 
, denn die Steigung der Tangente bei x = 0 soll schließlich gleich 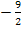sein. Es muss also gelten:
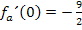
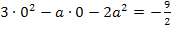
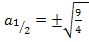
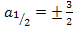
Damit ist die Aufgabe gelöst. Für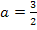 
und 
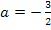verläuft bei x = 0 die Tangente an den Graph 
senkrecht zu der Geraden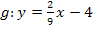 
.
6. Bsp.:Aus einer alten Schulaufgabe Gymnasium 11. Klasse
Gegeben ist die Funktionenschar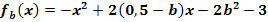 
mit x 
ℝ.
a.) Auf welcher Kurve liegen alle Hochpunkte dieser Schar? Gehört diese Kurve zur Schar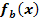 
?
b.) Wie viele gemeinsame Punkte kann die Gerade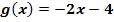 
mit einer Funktion der Schar 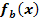höchstens haben? (Kurze Begründung!)
c.) Für welche Werte von b berühren die Funktionen der Schar 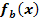jeweils die Gerade ?
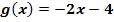Lösung:
Zu 6a.)
Geg.: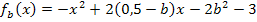 
Für den Parameter b ist nichts angegeben, also gilt:b ℝ
Bei der vorliegenden Schar handelt es sich um eine Schar quadratischer Funktionen, d.h. um eine Parabelschar.
Gesucht ist die Kurve, auf der alle Hochpunkte der Schar liegen, in anderen Worten die Ortskurve der Hochpunkte.
Berechnung der Ortskurve der HOP (1. Methode)
Wir berechnen zuerst die x- und y-Koordinate der Hochpunkte der Schar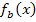 
.
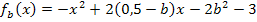
Dazu bilden wir die Ableitung der Funktionenschar.
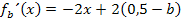
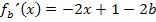
Beim Hochpunkt muss die Tangente waagrecht verlaufen. Die Steigung / Ableitung muss dort also gleich Null sein. Um die x-Koordinate des Hochpunktes zu berechnen, setzen wir die Ableitung gleich Null.
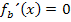
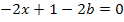
Indem wir diese Gleichung nach x auflösen, erhalten wir die gesuchte x-Koordinate.
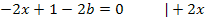
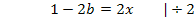
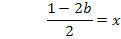
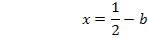
Die zugehörige y-Koordinate erhält man durch Einsetzen der berechneten x-Koordinate in die Gleichung der Schar .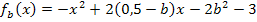
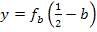
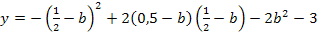
Der vorliegende Term muss noch vereinfacht werden. Die erste Klammer wird mit Hilfe der zweiten binomischen Formel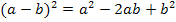 
quadriert. Die hinteren Klammern werden einfach ausmultipliziert. Danach fasst man soweit möglich zusammen.
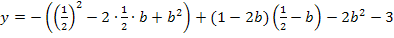
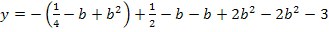
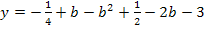
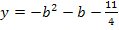
Alle Parabeln der Schar 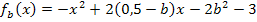mit b ℝ sind nach unten geöffnete Normalparabeln. (Das erkennt man daran, dass vor dem 
nur ein Minus steht. Vor dem steht also kein b und deshalb haben alle Parabeln der Schar den gleichen Öffnungsfaktor -1. Man sagt, der Öffnungsfaktor der Parabeln ist unabhängig vom Parameter b.
