Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

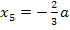Aus diesen Vorzeichen kann man dann auf das Steigungsverhalten von und auf die Art der Extrema schließen. Da sich sowohl bei als auch bei 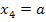das Vorzeichen der Ableitung ändert, liegt jeweils ein Extremum vor. Bei 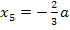wechselt das Vorzeichen von Plus nach Minus;d.h. zuerst steigt der Graph, danach fällt er. Es muss für a >0 bei 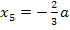ein relativer Hochpunkt vorliegen. (Bei 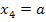liegt zwangsläufig ein relativer Tiefpunkt vor, was am Vorzeichenwechsel von Minus nach Plus erkennbar ist. Das war aber an sich gar nicht gefragt.)

1. Fall:a >0

Daraus folgt:

Für a >0 ist der Punkt relativer Hochpunkt von .

Nun verfahren wir entsprechend beim 2. Fall a <0. Hier noch einmal die zugehörige Tabelle:

2. Fall:a <0:

x		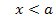a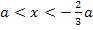
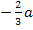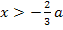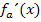		0		0

Für die Vorzeichenbestimmung von 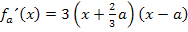arbeiten wir an sich wieder mit den gleichen „Beispielzahlen“ wie schon vorher beim 1. Fall. Da a jetzt aber für eine negative Zahl steht, ist 2a nun kleiner/negativer als a. 2a liegt daher für a <0 im Bereich 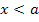. Für a <0 liegt 2a am Zahlenstrahl nämlich weiter links als a und somit ist dann 2a kleiner als a. (Bei negativen Werten von a ist im Prinzip alles genau umgekehrt wie bei positiven Werten von a.)

Aus dem Bereich 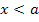nehmen wir deshalb die Zahl .

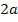Aus dem Bereich 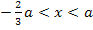nehmen wir wie schon beim 1. Fall die Zahl 0.

Aus dem Bereich 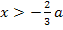nehmen wir .

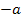Vom 1. Fall (siehe oben!) wissen wir:

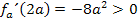
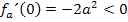
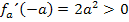
Daraus folgt für die Monotonie von :

2. Fall:a <0:

Für a <0 ist der Punkt relativer Tiefpunkt von .

Zusammenfassung:

Für a >0 ist der Punkt relativer Hochpunkt von .

Für a <0 ist der Punkt relativer Tiefpunkt von .

Zu 5e.)

Geg.: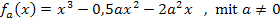

Es soll ermittelt werden, für welche Werte von a die Tangente an an der Stelle x = 0 senkrecht zur Geraden 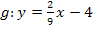verläuft.

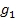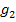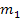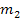Zur Erinnerung:Zwei Geraden und sind genau dann zueinander senkrecht, wenn für ihre Steigungen und gilt:

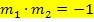
Wenn man diese Formel nach 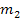auflöst, ergibt sich:

Das bedeutet im Prinzip, dass man die Steigung 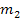ganz leicht ermitteln kann, wenn man 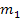kennt. Man muss bloßdas Vorzeichen von 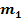umdrehen und den Kehrwert davon bilden. So erhält man die Steigung 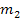der senkrechten Geraden.

In dieser Aufgabe hat die Gerade 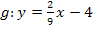die Steigung 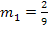. Die Tangente an an der Stelle x = 0 soll senkrecht zur Geraden 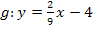verlaufen. Daher muss diese Tangente die Steigung 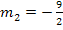haben. Die Steigung der Tangente entspricht der ersten Ableitung.

---