Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

Erste Ableitung (faktorisiert):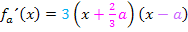

Nähere Erläuterungen, wie man einen Term im Allgemeinen faktorisiert, findest du bei:Faktorisierter Funktionsterm(In unserem Beispiel wurde natürlich die erste Ableitung 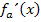faktorisiert und nicht die Funktionenschar selbst. Aber die prinzipielle Vorgehensweise beim Faktorisieren bleibt logischerweise gleich, ob man nun oder 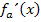faktorisiert.)

Wenn du selbst Schwierigkeiten beim Faktorisieren hast, arbeitest du bei der Vorzeichenermittlung für die Monotonietabelle doch besser mit der unfaktorisierten Form der Ableitung. Das ist zwar etwas mehr Rechenaufwand, funktioniert aber natürlich auch.

So, jetzt geht´s los mit der Ermittlung der Vorzeichen von 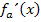in den einzelnen Bereichen. Wir beginnen mit dem Fall a >0. Hier noch einmal die zugehörige Tabelle:

1. Fall:a >0

x		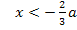		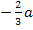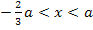a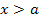
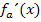		0		0

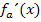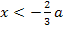Wir müssen nun jeweils die Vorzeichen von für , für 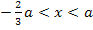und für 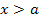ermitteln. Dazu wählen wir aus jedem der drei Bereiche eine „Beispielzahl“. Dabei ergibt sich jedoch das Problem, dass man nicht weiß, was a ist, und man deshalb nicht einfach mit richtigen Zahlen arbeiten kann. Was tun? Ganz einfach:Wir nehmen das a mit in unsere „Beispielzahl“ hinein.

Am besten lässt sich das an Hand des Bereichs 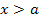erklären. Wir suchen dabei nach einer „Zahl“, die sicher größer ist als a. Solange a positiv ist – und das ist schließlich momentan der Fall – ist beispielsweise 2a oder 3a bestimmt größer als a. Als „Beispielzahl“ für den Bereich 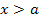bietet sich deshalb 2a oder 3a an.

Entsprechend geht man im Bereich 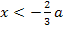vor. Für diesen Bereich wählt man am besten als Beispiel 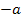oder 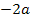, weil sowohl 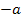als auch 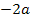kleiner ist als 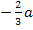. („Kleiner“ bedeutet „weiter links am Zahlenstrahl“.)

Für den Bereich 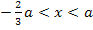nimmt man als „Beispielzahl“ am besten die Zahl 0. Die Null liegt sicher zwischen dem negativen Wert 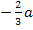und dem positiven Wert a;sie liegt also ganz bestimmt in dem Intervall und es lässt sich besonders einfach damit rechnen.

Wir entscheiden uns hier für die folgenden „Beispielzahlen“:

Aus dem Bereich 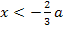nehmen wir .

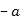Aus dem Bereich 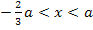nehmen wir 0.

Aus dem Bereich 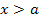nehmen wir .

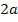Jetzt setzen wir die gewählten „Beispielzahlen“ in 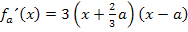ein und überlegen uns die jeweiligen Vorzeichen der Ableitung.

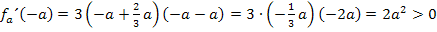
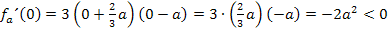
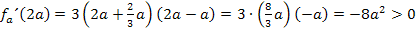
Nun können wir die jeweiligen Vorzeichen der Ableitung in die mittlere Zeile unserer Monotonietabelle eintragen.

---