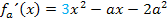Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

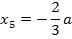
Nun erstellen wir eine Monotonietabelle. Dabei stellt sich die Frage, welche der beiden x-Koordinaten in der Monotonietabelle als erste, d.h. weiter links, eingetragen werden muss. Du weißt bestimmt, dass die x-Koordinaten ihrer Größe nach geordnet eingetragen werden müssen. Die kleinere steht immer weiter links, genauso wie an einem Zahlenstrahl. Jetzt ist natürlich die Frage zu beantworten, welche der beiden berechneten x-Koordinaten die kleinere und welche die größere ist. Was denkst du?

Vermutlich hast du dir nun Folgendes gedacht:Bei 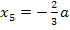steht ein Minus dabei und deshalb ist 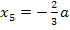negativ. Bei 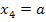steht kein Minus, also ist 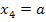positiv. Die negative x-Koordinate 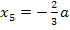ist logischerweise kleiner als die positive 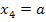und deshalb ist 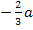kleiner als 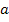. In der Monotonietabelle muss man also 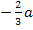links von a eintragen.

Diese Überlegung stimmt aber nur, wenn a positiv ist! Doch was ist, wenn a negativ ist? Dann ist alles genau umgekehrt! Das Vorzeichen der beiden ermittelten x-Koordinaten hängt also auch noch vom Vorzeichen von a ab!

Da man nicht allgemein sagen kann, welche der beiden x-Koordinaten die kleinere bzw. die größere ist, müssen wir eine Fallunterscheidung machen:

Für positive Werte von a ist 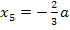negativ und somit kleiner als die positive x-Koordinate 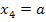. In der Monotonietabelle steht für a >0 die x-Koordinate 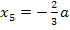links von .

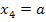Für negative Werte von a ist es allerdings genau umgekehrt, dann ist 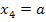negativ und 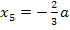positiv. Daher ist für a <0 die x-Koordinate 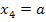kleiner als 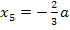. In der Monotonietabelle steht für a <0 die x-Koordinate 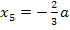rechts von .

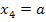Den Fall a = 0 müssen wir nicht bearbeiten, da laut Angabe gilt.

Wir müssen deswegen zwei verschiedene Monotonietabellen anfertigen, eine für a >0 und eine für a <0.

1. Fall:a >0

x		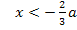		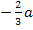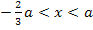a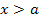
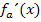		0		0

2. Fall:a <0:

x		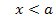a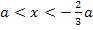
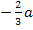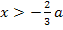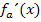		0		0

Um jeweils die Vorzeichen der ersten Ableitung herauszufinden, geht man am besten nicht von der Ableitung in der Form 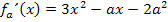aus, sondern von der faktorisierten Ableitung. Deshalb faktorisieren wir 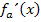jetzt. Wir wissen:Für 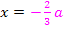und für 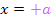wird die Ableitung Null. Die Ableitung muss deshalb die Linearfaktoren 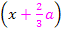und 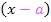haben. Beachte dabei die umgekehrten Vorzeichen! Außerdem darf man diejenige Zahl, die bei 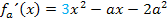vor der höchsten x-Potenz steht, also hier die Zahl 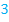, bei der faktorisierten Form der Ableitung nicht vergessen.

Erste Ableitung (unfaktorisiert):

---