Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

Als nächstes berechnen wir die zugehörige y-Koordinate. Dazu setzen wir die ermittelte x-Koordinate 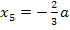in die Gleichung von ein.

Berechnung der y-Koordinate des zweiten Extremums:

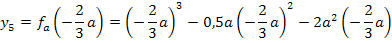
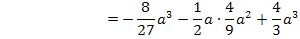
Nun wissen wir, dass im Punkt die Tangente an die Graphen der Schar waagrecht verläuft. Ob es sich bei diesem Punkt tatsächlich um ein Extremum handelt, wissen wir jedoch noch nicht;dies muss erst noch gezeigt werden. Außerdem sollen wir herausfinden, um was für ein Extremum es sich dabei handelt. Handelt es sich um einen relativen Hoch- oder Tiefpunkt der Schar ?

Das kann man auf zwei verschiedene Art und Weisen überprüfen, entweder mit dem Monotonieverhalten oder mit der zweiten Ableitung. Schüler, welche die zweite Ableitung im Unterricht noch nicht behandelt haben, müssen die Art des Extremums zwangsläufig mit dem Monotonieverhalten herausfinden. Allen anderen ist hier jedoch die Methode mit der zweiten Ableitung zu empfehlen;sie geht wesentlich schneller und einfacher.

Art des Extremums herausfinden

1. Methode (mit der zweiten Ableitung)

Die erste Ableitung 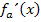haben wir bereits ermittelt;noch einmal Ableiten liefert die zweite Ableitung .

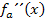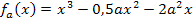
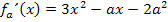
Nun wird die x-Koordinate des ermittelten Punktes in die zweite Ableitung eingesetzt;dadurch ergibt sich die Krümmung an dieser Stelle. Am Vorzeichen des Ergebnisses erkennt man, ob der Graph dort links- oder rechtsgekrümmt ist, also ob ein Hoch- oder Tiefpunkt vorliegt.

Zur Erinnerung:

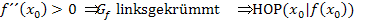
Wir setzen deshalb die x-Koordinate des zweiten Extremums 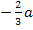für x in ein.

Welches Vorzeichen hat sich nun ergeben?

Nun denkst du dir bestimmt:Das Ergebnis ist 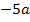und da steht ein Minus, also ist das Ergebnis negativ. Das ist so aber nicht korrekt!

Vorsicht:Das Ergebnis -5a ist nicht für alle zulässigen Werte von a negativ! Das Vorzeichen von -5a hängt nämlich auch vom Vorzeichen von a ab. Nur für positive Werte von a ist -5a negativ. Für negative Werte von a ist -5a dagegen positiv. Wir müssen also eine Fallunterscheidung machen. (Für a = 0 käme bei -5a sogar Null heraus. Aber es gilt hier laut Angabe . Den Fall a = 0 können wir daher vergessen.)

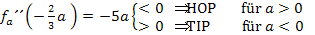
Daraus folgt:

Für a >0 ist der Punkt relativer Hochpunkt von .

Für a <0 ist der Punkt relativer Tiefpunkt von .

2. Methode (Ohne Verwendung der zweiten Ableitung)

Wir untersuchen das Monotonieverhalten der Schar .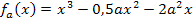

Aus der Gleichung 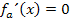haben wir die x-Koordinaten aller Punkte mit waagrechten Tangenten erhalten:

---