Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
1. Methode:Mit vorheriger Berechnung der y-Koordinate des Extremums

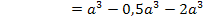
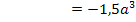
 Extremum bei
Extremum bei 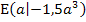
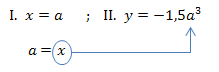
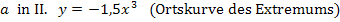
Definitionsmenge dieser Ortskurve:
Wegen  kann die x-Koordinate des Extremums
kann die x-Koordinate des Extremums  nicht den Wert Null annehmen. Deshalb gilt:
nicht den Wert Null annehmen. Deshalb gilt: 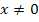
Die Lösung lautet deshalb:

2. Methode:Ohne vorheriger Berechnung der y-Koordinate des Extremums
Wir kennen die x-Koordinate des Extremums. Sie lautet:
![]()
Normalerweise würde man jetzt nach dem Parameter a auflösen, doch das ist hier gar nicht nötig. Es gilt schließlich:
![]()
Wir müssen bloßin  für a den Buchstaben x einsetzen, das Ganze vereinfachen und schon haben wir die gesuchte Ortskurve berechnet.
für a den Buchstaben x einsetzen, das Ganze vereinfachen und schon haben wir die gesuchte Ortskurve berechnet.
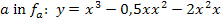
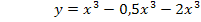
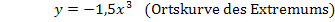
Außerdem ist gefragt, welcher Punkt der Ortskurve kein Extremum der Schar  ist. Wegen
ist. Wegen  kann die x-Koordinate des Extremums x = a niemals den Wert Null annehmen. Die Ortskurve ist somit nur für
kann die x-Koordinate des Extremums x = a niemals den Wert Null annehmen. Die Ortskurve ist somit nur für  definiert.
definiert.
Wir berechnen noch schnell die y-Koordinate des Punktes  der Ortskurve
der Ortskurve 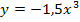 , der kein Extremum der Schar sein kann.
, der kein Extremum der Schar sein kann.
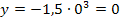
Der Punkt  kann somit kein Extremum der Schar
kann somit kein Extremum der Schar 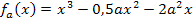 mit
mit  sein.
sein.
Hinweis:Für 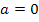 würde sich die Funktion
würde sich die Funktion  , also
, also  ergeben. Diese Funktion hat bei x = 0 eine dreifache Nullstelle, also den Terrassenpunkt
ergeben. Diese Funktion hat bei x = 0 eine dreifache Nullstelle, also den Terrassenpunkt  . Da ein Terrassenpunkt nicht zu den Extrempunkten zählt, würde sich auch für
. Da ein Terrassenpunkt nicht zu den Extrempunkten zählt, würde sich auch für 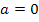 bei
bei  kein Extremum ergeben. Der Ursprung ist somit für keinen reellen Wert von a ein Extremum der Schar
kein Extremum ergeben. Der Ursprung ist somit für keinen reellen Wert von a ein Extremum der Schar 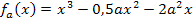 .
.
Zu 5d.)
Es ist die Art und Lage des zweiten Extremums der Schar 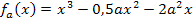 mit
mit  zu berechnen. Das erste Extremum liegt laut Teilaufgabe 5a.) bei x = a;wir suchen also genau das andere Extremum. Dazu bilden wir vorweg die erste Ableitung der Schar.
zu berechnen. Das erste Extremum liegt laut Teilaufgabe 5a.) bei x = a;wir suchen also genau das andere Extremum. Dazu bilden wir vorweg die erste Ableitung der Schar.
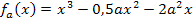
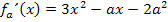
Berechnung der x-Koordinaten aller Punkte mit waagrechten Tangenten:
Bei einem Extremum verläuft die Tangente an den Graphen waagrecht. Die Steigung / erste Ableitung muss dort also gleich Null sein.
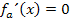
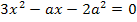
Die vorliegende Gleichung enthält  , x (ohne Potenz) und eine Konstante;sie ist also gemischtquadratisch. Mit der Mitternachtsformellässt sich eine gemischtquadratische Gleichung leicht lösen. Weil wir die Bezeichnungen
, x (ohne Potenz) und eine Konstante;sie ist also gemischtquadratisch. Mit der Mitternachtsformellässt sich eine gemischtquadratische Gleichung leicht lösen. Weil wir die Bezeichnungen 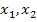 und
und  in Teilaufgabe 5b.) bereits für die Nullstellen der Schar verwendet haben, verwenden wir nun die Bezeichnungen
in Teilaufgabe 5b.) bereits für die Nullstellen der Schar verwendet haben, verwenden wir nun die Bezeichnungen 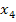 und
und 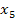 für die Lösungen dieser Gleichung.
für die Lösungen dieser Gleichung.
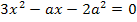
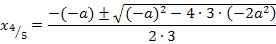
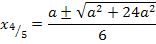



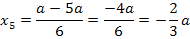
Offensichtlich ist 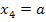 das bereits bekannte Extremum. Entsprechend muss wohl bei
das bereits bekannte Extremum. Entsprechend muss wohl bei 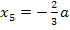 das gesuchte zweite Extremum der Schar
das gesuchte zweite Extremum der Schar 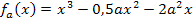 mit
mit  liegen.
liegen.

