Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Nun stellen wir die zwei Gleichungen I. und II. auf, die sich aus den oben schon erwähnten Informationen I. und II. ergeben. Damit können wir die Parameter b und c (zumindest in Abhängigkeit von a) berechnen.
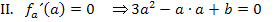
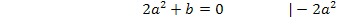
Nun müssen wir nur noch die ermittelten Ergebnisse für b und c in die gegebene Schar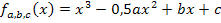 
einsetzen. So kommt man auf die Gleichung der gesuchten Schar. Sie lautet:
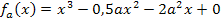
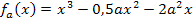
Zu 5b.)
Es soll gezeigt werden, dass alle Funktionen der Schar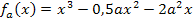 
mit 
und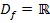 
genau drei Nullstellen besitzen. Deshalb rechnen wir die Nullstellen erst einmal aus, indem wir 
gleich Null setzen. Dabei rechnen wir natürlich in Abhängigkeit von a. Du stellst dir also weiterhin vor, a sei irgendeine konkrete Zahl. Dann rechnest du die Nullstellen von aus, natürlich ohne wirklich eine bestimmte Zahl für a einzusetzen.
Nst.: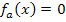 
Obwohl bei dieser Gleichung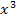 
vorkommt, muss keine Polynomdivision durchgeführt werden. Weil dabei keine Konstante (d.h. Zahl ohne x) vorkommt, kann x ausgeklammert werden. Dadurch entsteht eine Gleichung der Form „Produkt gleich Null“ und solche Gleichungen lassen sich bekanntlich lösen, indem man die Faktoren des Produkts einzeln gleich Null setzt. (Du weißt:Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist.)
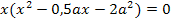
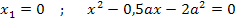
Die noch zu lösende gemischtquadratische Gleichung lösen wir mit der Mitternachtsformel.
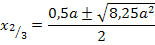
Im Prinzip muss man jetzt nicht mehr weiterrechnen, denn es ist bereits klar, dass sich für immer drei verschiedene Lösungen ergeben. Die Diskriminante ist hier nämlich 
. Wegen des Quadrats kann die Diskriminante sicher nicht negativ werden. Für a = 0 würde die Diskriminante zwar den Wert Null annehmen, aber es gilt . Für 
ist die Diskriminante immer positiv und es ergeben sich aus der gemischtquadratischen Gleichung zwei Lösungen. Es gibt also zusätzlich zur ersten Lösung 
immer zwei weitere Lösungen aus der gemischtquadratischen Gleichung.
Diskriminante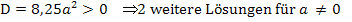 
Keine der beiden Lösungen der gemischtquadratischen Gleichung fällt für mit der ersten Lösung zusammen. (Nur für a = 0 würden hier alle drei Lösungen zu einer dreifachen Lösung zusammenfallen. Der Wert a = 0 ist hier aber nicht zugelassen.) Daher ergeben sich für immer drei verschiedene Nullstellen. Genau dies war zu beweisen.
Zu 5c.)
Gesucht ist die Gleichung der Ortskurve des in Teilaufgabe 5a.) angegebenen Extremums. In 5a.) war angegeben, dass bei x = a ein Extremum der Schar 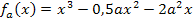mit liegt. Die y-Koordinate des Extremums ist noch nicht bekannt. Es stehen uns die zwei oben beschriebenen Methoden zur Verfügung die Ortskurve des erwähnten Extremums zu berechnen:Mit oder ohne vorheriger Berechnung der zugehörigen y-Koordinate.
