Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
(Wenn es dir leichter fällt, kannst du den Faktor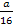 
aber auch zusammen mit dem 
in die Klammer hineinmultiplizieren, bevor du ableitest.)
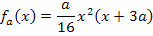
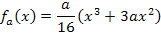
Erste Ableitung bilden:(Siehe auch:Einfache Ableitungsregeln)
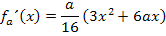
Wir klammer dabei den Faktor 3x aus. Das ergibt:
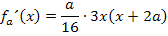
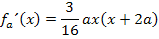
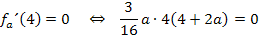
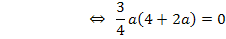
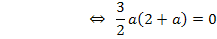
Nun müssen wir diese Gleichung nach a auflösen. Wie würdest du das machen? Vielleicht die linke Seite ausmultiplizieren?
Das wäre keine gute Idee! Wenn du die linke Seite der Gleichung ausmultiplizierst, machst du dir die Sache bloßschwerer:Dann könntest du zwar nachher die Mitternachtsformel anwenden, doch geht es anders viel schneller. Die Gleichung hat nämlich die Form „Produkt gleich Null“ und solche Gleichungen lassen sich ganz einfach lösen:Ein Produkt ist doch gleich Null, wenn einer der Faktoren gleich Null ist. Du kannst deshalb die Faktoren des Produkts einzeln gleich Null setzen. D.h. du kannst hier einfach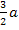 
und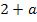 
jeweils einzeln gleich Null setzen. Du musst dich also bloßfragen, für welchen Wert von a wird der erste Faktor 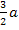gleich Null und für welchen Wert von a wird der zweite Faktor 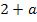gleich Null.
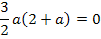
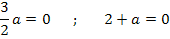
Der erste Faktor wird natürlich nur dann gleich Null, wenn man für a Null einsetzt;da aber laut Angabe 
gilt, kann a = 0 nicht unsere gesuchte Lösung sein. Deshalb ist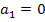 
oben eingeklammert. Der zweite Faktor 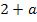wird gleich Null für 
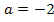. Das ist also der einzige Wert von a, für den die Bedingung „waagrechte Tangente bei x = 4“ erfüllt ist. Den Wert 
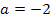muss man noch in die Gleichung von 
einsetzen. Das ergibt die gesuchte Funktion.
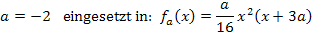
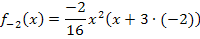
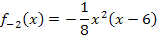
Zu 1c.)
Geg.: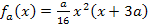 
mit
Gesucht sind diejenigen Werte von a, für welche die Tangente an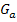 
im Punkt 
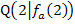parallel zu der Geraden 
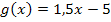verläuft. Wie du sicher weißt, sind zwei Geraden genau dann parallel zueinander, wenn sie die gleiche Steigung haben. Die Gerade 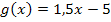besitzt offensichtlich die Steigung m = 1,5. Also muss auch die Tangente an 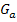im Punkt 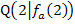die Steigung m = 1,5 haben. Die Steigung der Tangente von 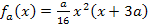an der Stelle x = 2 entspricht bekanntlich der ersten Ableitung an dieser Stelle. Deshalb muss gelten:
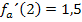
Die erste Ableitung der Schar haben wir bei 1b.) bereits ermittelt. Sie lautet:
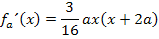
Wegen 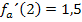müssen wir jetzt bei 
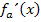die Zahl 2 für x einsetzen und das Ergebnis gleich 1,5 setzen. So bekommen wir eine Gleichung, mit der wir die gesuchten Werte von a berechnen können.
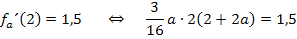
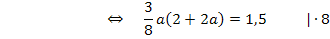
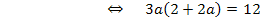
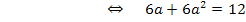
Es handelt sich um eine gemischtquadratische Gleichung;es kommt schließlich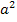 
und a in der Gleichung vor.
