Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
)
Gegeben ist die in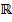 
definierte Schar 
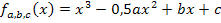mit den drei reellen Parametern a, b und c, wobei gilt: 
In anderen Worten:Die Parameter a, b und c können irgendwelche Zahlen sein, nur a kann nicht gleich Null sein, b und c aber schon.
Es ist die Gleichung der Funktionenschar 
zu berechnen, deren Scharkurven durch den Ursprung des Koordinatensystems verlaufen und an der Stelle x = a ein Extremum haben. Der Parameter a soll hier nicht explizit ermittelt werden;es soll schließlich eine Schar herauskommen und das bedeutet, dass der Parameter a in der Gleichung von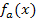 
noch vorkommen muss. Man soll also b und c eventuell in Abhängigkeit von a so berechnen, dass die genannten Bedingungen erfüllt sind. (In den Ergebnissen von b und c kann also noch der Parameter a auftreten, muss es aber nicht.) Um alle drei Parameter a, b und c wirklich ausrechnen zu können, sind in der Angabe sowieso nicht genug Informationen enthalten. Um drei Unbekannte bestimmen zu können, bräuchte man nämlich drei Gleichungen, also drei Informationen in der Aufgabenstellung. Hier sind aber nur zwei Informationen gegeben:
I. Die Scharkurven verlaufen alle durch den Koordinatenursprung;d.h. der Punkt (0|0) liegt auf allen Graphen der Schar .
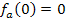
II. Die Scharkurven haben an der Stelle x = a ein Extremum;d.h. bei x = a verläuft die Tangente an die Graphen der Schar waagrecht. Somit ist die Steigung, also die erste Ableitung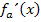 
bei x = a gleich Null.
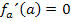
Eine dritte Information gibt es hier nicht. Einen der drei Parameter a, b und c kann man deshalb nicht ausrechnen. Die anderen beiden können allerdings zumindest in Abhängigkeit vom dritten Parameter ermittelt werden. Dass man hier in Abhängigkeit von a rechnen muss, also genau die Parameter b und c (eventuell in Abhängigkeit von a) berechnen soll, ergibt sich daraus, dass nach einer Schar gefragt ist und nicht nach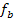 
oder 
. Der Parameter, der am Schluss noch in der Gleichung von auftreten soll, ist offensichtlich a. Du musst also bei der folgenden Rechnung so tun, als wäre a eine richtige Zahl, auch wenn du a gar nicht kennst. Nur die Parameter b und c sind gesucht.
Berechnung von b und c (eventuell in Abhängigkeit von a):
Hier noch einmal die gegebene Schar:
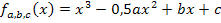
Wir bilden vorweg die erste Ableitung in Abhängigkeit von a und b. (Der dritte Parameter c fällt beim Ableiten weg.)
