Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
) Daher gilt für die x-Koordinate des rechten Wendepunktes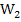 
: 
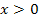
Jetzt dürfen wir aber den anderen Wendepunkt (d.h. den Terrassenpunkt) nicht vergessen. Auch ein Terrassenpunkt ist ein Wendepunkt, nur dass dort die Wendetangente eben waagrecht verläuft. Der Terrassenpunkt hat unabhängig von k die Koordinaten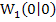 
. Auch dieser Punkt liegt auf der Funktion 
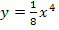, was sich mit 
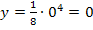leicht nachweisen lässt. 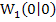gehört also auch noch zu der Funktion 
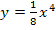. Der Punkt 
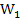hat die x-Koordinate x = 0. Deshalb ist die Ortskurve 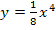auch bei x = 0 definiert.
Insgesamt ergibt sich somit die Definitionsmenge der Ortskurve: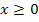 
Die Ortskurve der WEP der Schar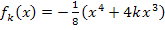 
mit 
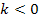hat die Gleichung:
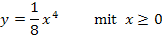
Damit ist diese Aufgabe gelöst. Gleich weiter mit dem nächsten Aufgabenbeispiel. Darin werden wir uns zum ersten Mal mit einer Funktionenschar beschäftigen, die mehrere verschiedene Parameter enthält. Bisher hatten wir es immer mit einparametrigen Scharen zu tun;d.h. die Gleichung der Schar enthielt bisher immer genau einen Scharparameter, also nur einen anderen Buchstaben neben der Variablen x. Im 5. Beispiel kommt nun eine dreiparametrige Schar vor, also eine Schar mit 3 verschiedenen Parametern a, b und c.
Aber keine Sorge, du musst keine komplette Kurvendiskussion einer Schar mit mehreren Parametern beherrschen. Zwei der drei Parameter der Schar im 5. Bsp. werden in Teilaufgabe 5a.) sofort explizit berechnet, so dass für alle weiteren Teilaufgaben doch nur eine einparametrige Schar übrig bleibt.
Bei einer Funktionenschar mit zwei oder mehr Parametern musst du in der Schule normalerweise nie eine Kurvendiskussion durchführen. Die notwendigen Fallunterscheidungen würden nämlich den Zeitrahmen einer Klausur oder der Abiturprüfung komplett sprengen. (Das wäre eher etwas für eine Seminararbeit im Fach Mathematik.)
5. Bsp.:
Wir betrachten die dreiparametrige Schar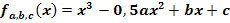 
mit a, b, c 
, 
, 
.
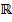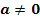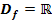a.) Bestimme die Gleichung der Funktionenschar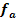 
, deren Scharkurven alle durch den Ursprung des Koordinatensystems verlaufen und jeweils an der Stelle x = a ein Extremum haben. (Ergebnis: 
)
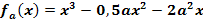b.) Zeige, dass alle Funktionen der Schar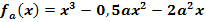 
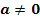mit und 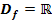genau drei Nullstellen besitzen!
c.) Bestimme die Gleichung der Ortskurve des in a.) angegebenen Extremums! Welcher Punkt der Ortskurve ist kein Extremum der Schar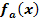 
?
d.) Ermittle Art und Lage des zweiten Extremums der Schar !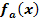
e.) Für welche Werte von a verläuft die Tangente an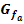 
an der Stelle x = 0 senkrecht zur Geraden 
?
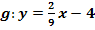Lösung:
Zu 5a.
