Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Deshalb gilt auch für k = -1 der Terrassenpunkt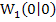 
.
Diese Teilaufgabe ist jetzt eigentlich gelöst;eine Zeichnung ist an sich nicht verlangt. Damit du dir das Ganze aber besser vorstellen kannst, hier zusätzlich noch eine Abbildung, in der du den Graph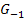 
zu k = -1 (in Hellblau) zusammen mit einigen anderen Graphen der Schar 
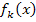mit k <0 (in Dunkelblau) sehen kannst. Die zu 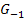gehörige Wendetangente im Wendepunkt 
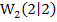ist lila gezeichnet. Nur diese Wendetangente verläuft parallel zu der Geraden y = 2x + 3 (schwarz gestrichelt). Die anderen Wendetangenten sind nicht dargestellt, doch dürfte dir klar sein, dass sie alle jeweils deutlich flacher oder steiler verlaufen als die schwarz gestrichelte Gerade.
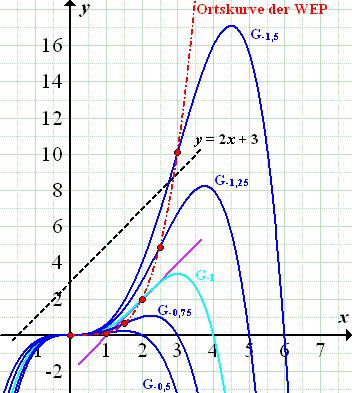
Abb.:Einige ausgewählte Graphen der Schar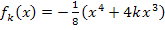 
. In Dunkelblau die Graphen zu 
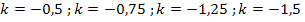und in Hellblau der in dieser Teilaufgabe gesuchte Graph 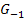mit 
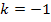. Bei den rot markierten Punkten handelt es sich um die Wendepunkte der gezeigten Scharfunktionen. Sie liegen alle auf der rot gestrichpunkteten Linie. Die rot gestrichpunktete Linie stellt somit die Ortskurve der Wendepunkte dar. (Ihre Gleichung sollst du in der nächsten Teilaufgabe selbst ermitteln, daher wird die Gleichung dieser Ortskurve jetzt noch nicht verraten.)
Zu 4d.)
Gesucht ist die Gleichung der Kurve, auf der alle Wendepunkte der Schar 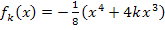mit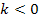 
liegen, also die Ortskurve der Wendepunkte.
In 4c.) haben wir bereits die Koordinaten der Wendepunkte von 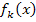in Abhängigkeit von k ermittelt. Sie lauten:
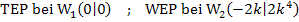
Nur der Punkt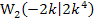 
kommt für die Berechnung der Ortskurve der WEP in Frage, da nur er abhängig ist von k. Die y-Koordinate dieses Wendepunktes ist bereits bekannt, so dass wir die Ortskurve am schnellsten nach unserer 1. Methode finden.
Vergleiche oben:Ortskurve ermitteln (1. Methode)
Sowohl bei der x-Koordinate als auch bei der y-Koordinate von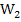 
kommt der Scharparameter k vor. Deshalb müssen wir k eliminieren, um die Gleichung der Ortskurve der WEP zu erhalten.
Aus 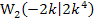folgt:
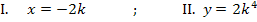
Wir lösen Gleichung I. nach k auf und setzen das Ergebnis für k in Gleichung II. ein.
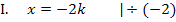
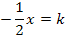
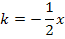
Einsetzen von k in II. ergibt:
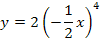
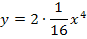
Nun wissen wir, dass die Punkte 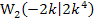alle auf der Funktion 
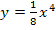liegen. Das ist also die Gleichung der gesuchten Ortskurve. Nun fehlt nur noch die Definitionsmenge dieser Ortskurve. Für die Schar 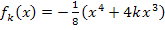gilt in dieser Teilaufgabe 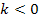. Daher kann die x-Koordinate des Wendepunktes 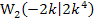ausschließlich positive Werte annehmen. Für 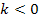ergibt sich schließlich: 
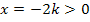(Die Zahl -2 mit einer negativen Zahl multipliziert ergibt logischerweise immer etwas Positives.
