Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Wir setzen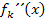 
gleich Null und lösen die Gleichung nach x auf.
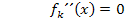
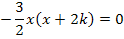
Wir können die Faktoren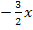 
und 
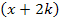einzeln gleich Null setzen, weil ein Produkt gleich Null ist, wenn einer der Faktoren Null ist.
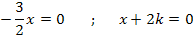
Dass es sich dabei tatsächlich um Wendestellen handelt, müssen wir hier ausnahmsweise nicht nachweisen, da in der Aufgabenstellung bereits erwähnt ist, dass es für k <0 immer zwei Wendepunkte gibt. Andere Punkte kommen nicht in Frage, denn für einen Wendepunkt muss zwangsläufig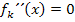 
gelten. Es muss sich demnach bei 
und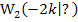 
definitiv um Wendepunkte handeln.
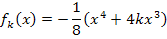
Berechnung der y-Koordinaten der WEP:
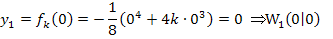
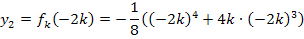
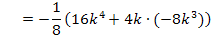
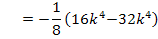
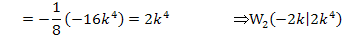
Art der Wendepunkte:
Es muss jeweils überprüft werden, ob es sich um einen normalen Wendepunkt WEP oder um Terrassenpunkte TEP (= WEP mit waagrechter Tangente) handelt. Bei einem Terrassenpunkt ist neben der zweiten Ableitung auch die erste Ableitung gleich Null (wegen der waagrechten Tangente). Bei einem normalen Wendepunkt ist im Gegensatz dazu die erste Ableitung ungleich Null, weil die Wendetangente dort nicht waagrecht verläuft. Wir setzen die ermittelten x-Koordinaten daher in die erste Ableitung ein und überprüfen, ob sich dabei (für k <0) Null ergibt oder nicht.
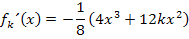
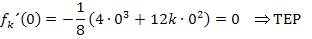
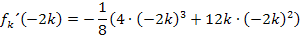
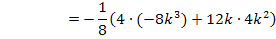
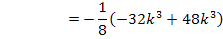
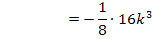
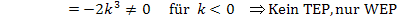
Zwischenergebnis:
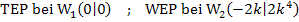
Als nächstes ist zu berechnen, für welchen Wert von k mit k <0 die Wendetangente im rechten Wendepunkt parallel zu der Geraden y = 2x + 3 verläuft. Wegen k <0 ist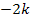 
ein positiver Wert. Daher ist für k <0 der Punkt 
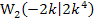der rechte Wendepunkt. Damit die Tangente in diesem Wendepunkt parallel zu y = 2x + 3 verläuft, muss die Steigung der zugehörigen Wendetangente ebenfalls den Wert 2 haben. (Die Gerade y = 2x + 3 hat schließlich die Steigung m = 2 und zwei Geraden sind nur dann parallel, wenn sie die gleiche Steigung haben.) Die Steigung der Wendetangente in 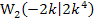entspricht bekanntlich der ersten Ableitung an dieser Stelle. Deshalb muss gelten:
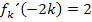
Oben haben wir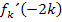 
bereits in Abhängigkeit von k berechnet: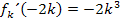 
Wir müssen jetzt bloßnoch herausfinden, für welchen Wert von k der Term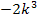 
genau 2 ergibt.
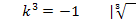
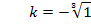
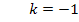
Das ist der gesuchte Wert von k. Für k = -1 verläuft die Tangente im rechten Wendepunkt der Schar parallel zu der Geraden y = 2x + 3. Für diesen Wert von k sollen außerdem Art und Koordinaten der Wendepunkte angegeben werden. Dazu setzen wir einfach den Wert k = -1 in 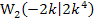ein. So erhält man für k = -1 den Wendepunkt 
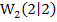. Der andere Wendepunkt ist ein Terrassenpunkt;er liegt unabhängig von k bei 
.
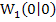