Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Gesucht sind die Nullstellen der Schar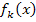 
in Abhängigkeit von k und ihre Vielfachheiten. Die Nullstellen einer Funktion berechnet man bekanntlich, indem man den Funktionsterm gleich Null setzt und die dadurch entstandene Gleichung nach x auflöst. Entsprechend geht man auch bei einen Funktionenschar vor.
Aber Vorsicht:Am Schluss der Nullstellenberechnung ist bei Funktionenscharen meist eine Fallunterscheidung nötig!
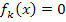
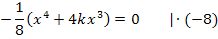
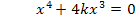
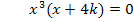
Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist. Daher können wir die Faktoren einzeln gleich Null setzen.
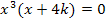
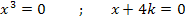
Jetzt denkst du dir vielleicht, dass es sich bei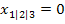 
um eine dreifache Nullstelle und bei 
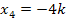um eine einfache Nullstelle von 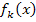handelt. Das ist aber nicht immer korrekt! Nur für 
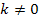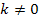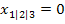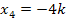gibt es hier zwei verschiedene Nullstellen, eine dreifache und eine einfache Nullstelle, weil nur für die beiden Lösungen nicht zusammenfallen. Für k = 0 fallen dagegen die beiden Lösungen und zusammen zu einer vierfachen Nullstelle. Bei der Schar 
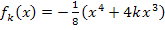gilt aber laut Angabe 
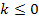. Das heißt, dass der Scharparameter k auch gleich Null sein kann. Wir müssen daher folgende Fallunterscheidung machen:
Für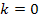 
:Eine vierfache Nullstelle bei x = 0
Für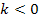 
:Zwei Nullstellen: 
(dreifach) und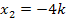 
(einfach)
Anmerkung:Laut Angabe gilt hier 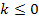, deshalb interessiert uns k >0 nicht weiter. Die Angabe über den Scharparameter 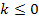ist sehr wichtig. Du solltest sie gleich von Anfang an beim Abschreiben der Angabe auf dein Blatt schreiben. Auch von den zulässigen Werten von k hängt es nämlich ab, ob in der jeweiligen Aufgabe eine Fallunterscheidung gemacht werden muss oder nicht. Hätte beispielsweise 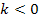oder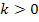 
gegolten, hätte man in diesem Beispiel auf die Fallunterscheidung verzichten können, weil dann der Fall k = 0 sowieso schon ausgeschlossen gewesen wäre.
Zu 4c.)
Ab sofort gilt:k <0
In der Angabe steht, dass für k <0 zwei verschiedene Wendepunkte von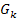 
existieren. Nun soll k so berechnet werden, dass die Wendetangente an 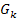im rechten Wendepunkt parallel zur Geraden 
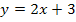verläuft. Außerdem sollen in Abhängigkeit von k und für den vorher ermittelten Wert von k auch die Art und Koordinaten der Wendepunkte angegeben werden.
Um diese Teilaufgabe zu lösen, musst du zuerst die Wendepunkte in Abhängigkeit von k berechnen.
Berechnung der Wendepunkte in Abhängigkeit von k:
Wir bilden vorweg die ersten beiden Ableitungen.
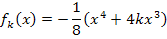
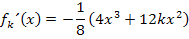
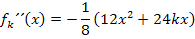
Wenn man bei der zweiten Ableitung 12x ausklammert, erhält man:
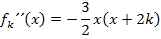
In dieser Form lassen sich die x-Koordinaten der Wendepunkte leicht ausrechnen.
